SCHEME OF WORK
WEEK TOPIC
1. Revision of first term work
2. Simple Equations involving Fractions: Simple Equations involving fractions. Word problems leading to simple equations involving fractions
3. Simultaneous Linear equations: Compilations of tables of values. Graphical solution of simultaneous linear equations in two variables.
4. Solution of simultaneous linear equations: Method by elimination and method by substitution.
5. Similar shapes: identification of similar figures-triangles, rectangles, squares, cubes and cuboids. Enlargement and scale factor
6. Use of scale factor in calculating lengths, areas and volumes of similar figures.
7. Trigonometry: the sine, cosine and tangent of an acute angle. Applications of Trigonometrical ratios to finding distances and lengths
8. Area of plane Figures: Area of plane figures-Triangles, parallelogram, trapezium and circle. Calculations of the areas of lands
9. Construction: Bisection of a segment-using a pair of compasses and a ruler. Bisection of an angle. Construction of angles 90[sup]0[/sup], 45[sup]0[/sup], 60[sup]0[/sup] and 30[sup]0[/sup]. Copying giving angles. Solving quantitative reasoning aptitude problems on construction.
10. Revision.
2ND TERM
WEEK 1
TOPIC: EQUATIONS WITH FRACTIONS.
CONTENTS:
Solving simple equations with fractions
Word problems leading to fractions
Word problems leading to equations with fractions
SIMPLE EQUATIONS WITH FRACTIONS
Equations such as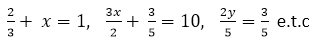
are equations involving fractions.
To solve any of these equations, we consider the L.C.M of the denominators and multiply each term of the equation by the L.C.M to clear the fractions and solve the equation as usual.
Example 1
Solve the equation: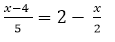
Solution
The denominators of the fractions in this equation are; 5 and 2.
L.C.M of 5 and 2 is 10.
Opening brackets we have,
2x- 8 = 20 - 5x
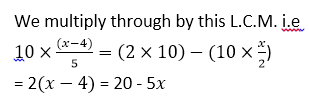
Collecting like terms we have,
5x + 2x = 20 +8
7x = 28.
Thus, x = [sup]28[/sup]/[sub]7[/sub] = 4
Example 2
Solve [sup]2x[/sup]/[sup]3[/sup] + [sup]4[/sup]/[sub]5[/sub]= [sup]17[/sup]/[sub]15[/sub]
Solution
The denominators are 3, 5 and 15.
Their L.C.M is 30
Thus, 30 x [sup]2x[/sup]/[sub]3[/sub] + 30 x [sup]4[/sup]/[sub]5[/sub]=30× [sup]17[/sup]/[sub]15[/sub]
10 x 2x + 6 x 4 = 2 x 17
20x + 24 = 34
20x=34-24=10
20x=10
x= [sup]10[/sup]/[sub]20[/sub]= 1/2
EVALUATION
Solve
(a)[sup]1[/sup]/[sub]y[/sub]+ [sup]1[/sup]/[sub]5[/sub]= [sup]1[/sup]/[sub]3[/sub] (b) [sup]5[/sup]/[sub]8[/sub]= [sup]10[/sup]/[sub]x[/sub] (c) [sup](y-5)[/sup]/[sub]4[/sub] = 8
NOTE: Sometimes it is not necessary to find the L.C.M of the denominators. If the equation has a single denominator on both sides of the equation, we simply solve the equation by cross multiplying as illustrated in the next example below.
Example 4
Solve [sup]2[/sup]/[sub](m-3)[/sub] = [sup]3[/sup]/[sub](2m-1)[/sub]
Solution
Cross multiplying, we have,
2(2m-1) =3(m-3)
Opening brackets, we have,
4m-2=3m-9
Collecting like terms
4m-3m=2-9
m= -7
WORD PROBLEMS INVOLVING FRACTIONS.
When solving word problems, identify the unknown and represent it by any letter of the alphabet. Form an equation in terms of the unknown based on the given information and solve the equation. Study the table below
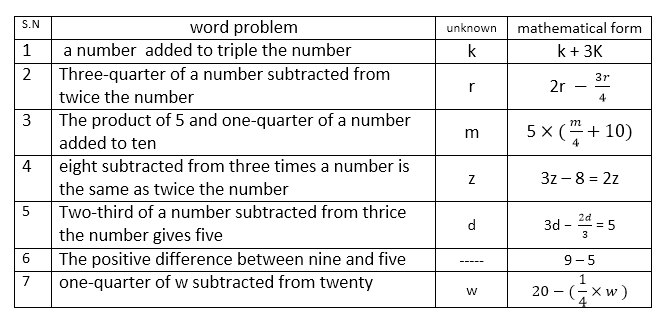
EVALUATION
Write the following in mathematical form
i. The positive difference between 2a and 5b
ii. One-third of a number subtracted from n gives ten
iii. Five times m plus twice n gives ten z
iv. The product of two-fifth of k and two
v. one-fourth of the product of eight and five
vi. Three-fifth of the difference between four and y
Example 4
A fisherman had 30 fish in his net. He ate some of them and discovered that there are 19 fish left. How many did he eat?
Solution
Total number of fish in the net = 30.
Let number of fish eaten = x
Number of fish left in the net = 19
Hence, 30 -x = 19
Or x = 30 – 19 = 11. Hence the man ate 11 fish
Example 5
The sum of the ages of a man and his son is 56 years. In 8 years time, the ratio of their ages will be 13:5. (a) How old are they now (b) find the difference between their ages.
Solution
(a) Let the age of the man be m years.
Therefore the son’s age will be (56 – m) years.
In 8 years time, their ages will be( 8 + m) years (man)
and (8 +56 – m) years (son).
The ratio of their ages at this time is 13:5.
Hence, [sup](8+m)[/sup]/[sub](8+56-m)[/sub] = [sup]13[/sup]/[sub]5[/sub]
Cross multiplying,
we have 5(8 + m) = 13( 64 – m)
Opening brackets,
40 + 5m = 832 – 13m
Collecting like terms,
5m + 13m = 832 - 40
18m = 792
m= [sup]792[/sup]/[sub]18[/sub] = 44.
Hence, the man’s age is 44 years and the son’s age is 56 – 44 = 12 years.
(b) The difference between their ages is 44 – 12 = 32
Example 6
When a certain number is subtracted from 56 and the result divided by 5, it is the same as if 14 is added to the number and the result divided by 2. Find the number
Solution
Let the number be n
The number subtracted from 56 is 56 – n
The result divided by 5 is [sup](56-n)[/sup]/[sub]5[/sub]
14 added to the number is n + 14
The result divided by 2 is [sup](n+14)[/sup]/[sub]2[/sub]
Hence, according to the given information,
[sup](56-n)[/sup]/[sub]5[/sub] = [sup](n+14)[/sup]/[sub]2[/sub]
Cross multiplying, we have,
2(56-n)=5(n+14)
Opening brackets,
112 – 2n = 5n + 70
Collecting like terms,
2n – 5n = 70 – 112
-3n=-42
n = [sup]42[/sup]/[sub]3[/sub] = 14
n = 14
EVALUATION:
i. Subtract 8 from 78, then find one-seventh of the result
ii. if I add 8 to a certain number and I double the result, my final answer is 36. What is the number?
ASSIGNMENT.
Refer to the following text books and do the following exercises
(1) (Work book, Nelson Functional Mathematics for Junior secondary school, book 3). Exercise E, Pages 9 and 10 questions 1 – 5.
(2) ( New General Mathematics for West Africa, for junior secondary school, U.B.E Edition Book 3). Exercise 2f, Page 26 Questions 1 – 5.
(3) ( Nelson Functional Mathematics. Book 3) Exercise 2.6 pages 34 and 35. Questions 1, 4 , 14 , 19 , 24
READING ASSIGNMENT.
New General Mathematics for West Africa, for junior secondary school, U.B.E Edition Book 3), Pages102-108
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Substitution Method
OBJECTIVE: At the end of the lesson, the students should be able to: Solve some problems on simultaneous equations by substitution method.
CONTENT:
Simultaneous Equation
Example 1: Solve the system of equation by substitution method
x - y = 3 .............(1)
2x + 3y=16...............(2)
Solution
Step 1
Solve one of the equations for one of its variables.
From equation (1), we solve for x
X =3 + y
Step 2
Substitute that quantity for the same variable in the other equation. In equation (2) we substitute for x.
2(3 + y) + 3y =16
6 + 2y + 3y = 16
Hence: 5y = 16 - 6
5y = 10
Y =2
To find x, substitute 2 for y in the equation.
X = 3 + y, that
X = 3 +2 =5
Therefore; x = 5
EVALUATION:
(1)
x + 2y = 6 ...................(1)
3x - y = -10.................(2)
(2)
x + 2y = 9 ...................(1)
3x - 4y = 7................. (2)
ASSIGNMENT: Answer the following questions
(1) 3x -2y =4...............(1)
X -4y =8................ (2)
(2) 2x - y =1 ...............(1)
2x -5y =-1............. (2)
further studies
http://www.themathpage.com/alg/simultan ... ations.htm
http://www.ict-teacher.com/Mathstutor/Equations.html
http://www.mrbartonmaths.com/algebra8.htm
practice test
http://quiz.econ.usyd.edu.au/mathquiz/s ... /quiz1.php
watch video
[youtube]http://www.youtube.com/watch?v=8ockWpx2KKI[/youtube]
[youtube]http://www.youtube.com/watch?v=it3vYdV_oyc[/youtube]
LESSON 38
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Substitution Method
OBJECTIVE: At the end of the lesson, the students should be able to:
Solve some problems on simultaneous equations by substitution method.
CONTENT:
Simultaneous Equation
Example 1: Solve the system of equation by substitution method
8X + 2Y = 13 .............(1)
16x + y =14 .................(2)
Solution
Expressing x in terms of y in equation 1,We get.
8x + 2y = 13
8x + 2y -2y =13 -2y subtract 2y from both sides
8x =13 -2y
X =13 -2y/8 divide both sides by 8
Replace x in equation 2 by, 13-2y/8
16(13 -2y)/8 + y = 14
2(13 -2y) + y = 14
26 -4y + y = 14
-3y = -12
Y = 4
Substitute the value of y in x =13 - 2y/8
We obtain x =13 -2(4)/8
X = 13 -8/8
X =5/8
EVALUATION: The lesson is evaluated as the students are asked to solve the following problems using substitution method.
(1) 2 x +3y = 8 ...................(1)
3x - 2 y = -1................ (2)
(2) 2x - y = 1 ................... (1)
2x - 5y =- 1................. (2)
ASSIGNMENT:
(1) 5y -7y =-22.................(1)
14x -5y =22................ (2)
(2) 3x - 2y =-13 ................(1)
3x -4y =17.................. (2)
further studies
http://www.revisionworld.co.uk/gcse-rev ... -equations
http://www.allaboutcircuits.com/vol_5/chpt_4/11.html
practice test
http://quiz.econ.usyd.edu.au/mathquiz/s ... /quiz2.php
http://quiz.econ.usyd.edu.au/mathquiz/s ... /quiz3.php
watch video
[youtube]http://www.youtube.com/watch?v=vYANxbSo3FA[/youtube]
[youtube]http://www.youtube.com/watch?v=R8ou4d-gjYo[/youtube]
CONTENTS:
Solving simple equations with fractions
Word problems leading to fractions
Word problems leading to equations with fractions
SIMPLE EQUATIONS WITH FRACTIONS
Equations such as
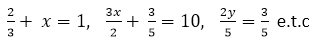are equations involving fractions. To solve any of these equations, we consider the L.C.M of the denominators and multiply each term of the equation by the L.C.M to clear the fractions and solve the equation as usual.
Example 1
Solve the equation:
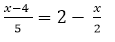
Solution
The denominators of the fractions in this equation are; 5 and 2.
L.C.M of 5 and 2 is 10.
Opening brackets we have,
2x- 8 = 20 - 5x
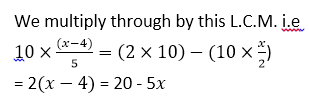
Collecting like terms we have,
5x + 2x = 20 +8
7x = 28.
Thus, x = [sup]28[/sup]/[sub]7[/sub] = 4
Example 2
Solve [sup]2x[/sup]/[sup]3[/sup] + [sup]4[/sup]/[sub]5[/sub]= [sup]17[/sup]/[sub]15[/sub]
Solution
The denominators are 3, 5 and 15.
Their L.C.M is 30
Thus, 30 x [sup]2x[/sup]/[sub]3[/sub] + 30 x [sup]4[/sup]/[sub]5[/sub]=30× [sup]17[/sup]/[sub]15[/sub]
10 x 2x + 6 x 4 = 2 x 17
20x + 24 = 34
20x=34-24=10
20x=10
x= [sup]10[/sup]/[sub]20[/sub]= 1/2
EVALUATION
Solve
(a)[sup]1[/sup]/[sub]y[/sub]+ [sup]1[/sup]/[sub]5[/sub]= [sup]1[/sup]/[sub]3[/sub] (b) [sup]5[/sup]/[sub]8[/sub]= [sup]10[/sup]/[sub]x[/sub] (c) [sup](y-5)[/sup]/[sub]4[/sub] = 8
NOTE: Sometimes it is not necessary to find the L.C.M of the denominators. If the equation has a single denominator on both sides of the equation, we simply solve the equation by cross multiplying as illustrated in the next example below.
Example 4
Solve [sup]2[/sup]/[sub](m-3)[/sub] = [sup]3[/sup]/[sub](2m-1)[/sub]
Solution
Cross multiplying, we have,
2(2m-1) =3(m-3)
Opening brackets, we have,
4m-2=3m-9
Collecting like terms
4m-3m=2-9
m= -7
WORD PROBLEMS INVOLVING FRACTIONS.
When solving word problems, identify the unknown and represent it by any letter of the alphabet. Form an equation in terms of the unknown based on the given information and solve the equation. Study the table below
EVALUATION
Write the following in mathematical form
i. The positive difference between 2a and 5b
ii. One-third of a number subtracted from n gives ten
iii. Five times m plus twice n gives ten z
iv. The product of two-fifth of k and two
v. one-fourth of the product of eight and five
vi. Three-fifth of the difference between four and y
Example 4
A fisherman had 30 fish in his net. He ate some of them and discovered that there are 19 fish left. How many did he eat?
Solution
Total number of fish in the net = 30.
Let number of fish eaten = x
Number of fish left in the net = 19
Hence, 30 -x = 19
Or x = 30 – 19 = 11. Hence the man ate 11 fish
Example 5
The sum of the ages of a man and his son is 56 years. In 8 years time, the ratio of their ages will be 13:5. (a) How old are they now (b) find the difference between their ages.
Solution
(a) Let the age of the man be m years.
Therefore the son’s age will be (56 – m) years.
In 8 years time, their ages will be( 8 + m) years (man)
and (8 +56 – m) years (son).
The ratio of their ages at this time is 13:5.
Hence, [sup](8+m)[/sup]/[sub](8+56-m)[/sub] = [sup]13[/sup]/[sub]5[/sub]
Cross multiplying,
we have 5(8 + m) = 13( 64 – m)
Opening brackets,
40 + 5m = 832 – 13m
Collecting like terms,
5m + 13m = 832 - 40
18m = 792
m= [sup]792[/sup]/[sub]18[/sub] = 44.
Hence, the man’s age is 44 years and the son’s age is 56 – 44 = 12 years.
(b) The difference between their ages is 44 – 12 = 32
Example 6
When a certain number is subtracted from 56 and the result divided by 5, it is the same as if 14 is added to the number and the result divided by 2. Find the number
Solution
Let the number be n
The number subtracted from 56 is 56 – n
The result divided by 5 is [sup](56-n)[/sup]/[sub]5[/sub]
14 added to the number is n + 14
The result divided by 2 is [sup](n+14)[/sup]/[sub]2[/sub]
Hence, according to the given information,
[sup](56-n)[/sup]/[sub]5[/sub] = [sup](n+14)[/sup]/[sub]2[/sub]
Cross multiplying, we have,
2(56-n)=5(n+14)
Opening brackets,
112 – 2n = 5n + 70
Collecting like terms,
2n – 5n = 70 – 112
-3n=-42
n = [sup]42[/sup]/[sub]3[/sub] = 14
n = 14
EVALUATION:
i. Subtract 8 from 78, then find one-seventh of the result
ii. if I add 8 to a certain number and I double the result, my final answer is 36. What is the number?
ASSIGNMENT.
Refer to the following text books and do the following exercises
(1) (Work book, Nelson Functional Mathematics for Junior secondary school, book 3). Exercise E, Pages 9 and 10 questions 1 – 5.
(2) ( New General Mathematics for West Africa, for junior secondary school, U.B.E Edition Book 3). Exercise 2f, Page 26 Questions 1 – 5.
(3) ( Nelson Functional Mathematics. Book 3) Exercise 2.6 pages 34 and 35. Questions 1, 4 , 14 , 19 , 24
READING ASSIGNMENT.
New General Mathematics for West Africa, for junior secondary school, U.B.E Edition Book 3), Pages102-108
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Substitution Method
OBJECTIVE: At the end of the lesson, the students should be able to: Solve some problems on simultaneous equations by substitution method.
CONTENT:
Simultaneous Equation
Example 1: Solve the system of equation by substitution method
x - y = 3 .............(1)
2x + 3y=16...............(2)
Solution
Step 1
Solve one of the equations for one of its variables.
From equation (1), we solve for x
X =3 + y
Step 2
Substitute that quantity for the same variable in the other equation. In equation (2) we substitute for x.
2(3 + y) + 3y =16
6 + 2y + 3y = 16
Hence: 5y = 16 - 6
5y = 10
Y =2
To find x, substitute 2 for y in the equation.
X = 3 + y, that
X = 3 +2 =5
Therefore; x = 5
EVALUATION:
(1)
x + 2y = 6 ...................(1)
3x - y = -10.................(2)
(2)
x + 2y = 9 ...................(1)
3x - 4y = 7................. (2)
ASSIGNMENT: Answer the following questions
(1) 3x -2y =4...............(1)
X -4y =8................ (2)
(2) 2x - y =1 ...............(1)
2x -5y =-1............. (2)
further studies
http://www.themathpage.com/alg/simultan ... ations.htm
http://www.ict-teacher.com/Mathstutor/Equations.html
http://www.mrbartonmaths.com/algebra8.htm
practice test
http://quiz.econ.usyd.edu.au/mathquiz/s ... /quiz1.php
watch video
[youtube]http://www.youtube.com/watch?v=8ockWpx2KKI[/youtube]
[youtube]http://www.youtube.com/watch?v=it3vYdV_oyc[/youtube]
LESSON 38
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Substitution Method
OBJECTIVE: At the end of the lesson, the students should be able to:
Solve some problems on simultaneous equations by substitution method.
CONTENT:
Simultaneous Equation
Example 1: Solve the system of equation by substitution method
8X + 2Y = 13 .............(1)
16x + y =14 .................(2)
Solution
Expressing x in terms of y in equation 1,We get.
8x + 2y = 13
8x + 2y -2y =13 -2y subtract 2y from both sides
8x =13 -2y
X =13 -2y/8 divide both sides by 8
Replace x in equation 2 by, 13-2y/8
16(13 -2y)/8 + y = 14
2(13 -2y) + y = 14
26 -4y + y = 14
-3y = -12
Y = 4
Substitute the value of y in x =13 - 2y/8
We obtain x =13 -2(4)/8
X = 13 -8/8
X =5/8
EVALUATION: The lesson is evaluated as the students are asked to solve the following problems using substitution method.
(1) 2 x +3y = 8 ...................(1)
3x - 2 y = -1................ (2)
(2) 2x - y = 1 ................... (1)
2x - 5y =- 1................. (2)
ASSIGNMENT:
(1) 5y -7y =-22.................(1)
14x -5y =22................ (2)
(2) 3x - 2y =-13 ................(1)
3x -4y =17.................. (2)
further studies
http://www.revisionworld.co.uk/gcse-rev ... -equations
http://www.allaboutcircuits.com/vol_5/chpt_4/11.html
practice test
http://quiz.econ.usyd.edu.au/mathquiz/s ... /quiz2.php
http://quiz.econ.usyd.edu.au/mathquiz/s ... /quiz3.php
watch video
[youtube]http://www.youtube.com/watch?v=vYANxbSo3FA[/youtube]
[youtube]http://www.youtube.com/watch?v=R8ou4d-gjYo[/youtube]
WEEK 2
TOPIC: SIMULTANEOUS LINEAR EQUATIONS
CONTENT:
Concept of simultaneous equations
Preparing table of values for variables
Graphical approach to the solution of simultaneous equations
SUB TOPIC: CONCEPT OF SIMULTANEOUS EQUATIONS
Equations such as
x-y= -1……………………..i
x+y=3……………………...ii
With two variables x and y to be solved at the same time are called simultaneous equations.
SUB TOPIC: PREPARING TABLE OF VALUES.
The above equations x-y= -1,x+y=3 are both linear equations with two variables. For a certain value of x, y has a corresponding value. For example, considering the equation x-y= -1, making y the subject of the formula,
y = x + 1.
When x takes the value 0, y=0+1=1, When x takes the value 1, y=1+1=2. When x takes the value 2, y=2+1=3. When x takes the value 3, y=3+1=4. The result can be displayed in a table as shown below
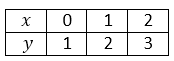
The table above is known as table of specification. The table can be extended if we assign more values to x
EVALUATION
a. Prepare table of specification for the equation y=3-x for x=0 to 2
b. Copy and complete the table for the relation y=[sup]1[/sup]/[sub]2[/sub] + x
SUB TOPIC: GRAPHICAL METHOD OF SOLVING SIMULTANEOUS EQUATIONS
This method involves creating tables of values for both variables or unknowns. y is usually made the subject of the formula and referred to as the dependent variable while x is the independent variable. Simple values can be assigned to x in order to determine the corresponding values of y. Although two plotted points are enough to draw the lines of both equations, it is advisable to plot at least three points. After plotting, the points are expected to lie on the same straight line for both equations. The lines should intersect at a point or this can be achieved by extending one or both lines with a ruler. The point of intersection of the lines gives the solutions of the simultaneous equations. If the lines are parallel, it means the simultaneous equations have no solution.
Example 1
Solve using graphical approach:
x-y= -1……………………..i
x+y=3………………………...ii
Solution
We assign four values to x (0, 1, 2 and 3) and use them to find the corresponding values of y for both equations.
Considering equation 1 (y=x+1).
When x = 0, y = 0 +1 = 1.
When x = 1, y = 1 + 1 = 2.
When x = 2, y = 2 + 1 = 3.
When x = 3, y = 3 +1 = 4.
y = x+1
x 0 1 2 3
y 1 2 3 4
Similarly, from equation ii,
y = 3 – x.
When x = 0, y = 3 – 0 = 3.
When x = 1, y=3-1=2.
When x = 2, y=3-2=1.
When x=3, y=3-3=0
y = 3-x
x 0 1 2 3
y 3 2 1 0
Using a scale of 2cm = 1 unit for both axes, we plot a graph of y against x for both equations. See the graph below
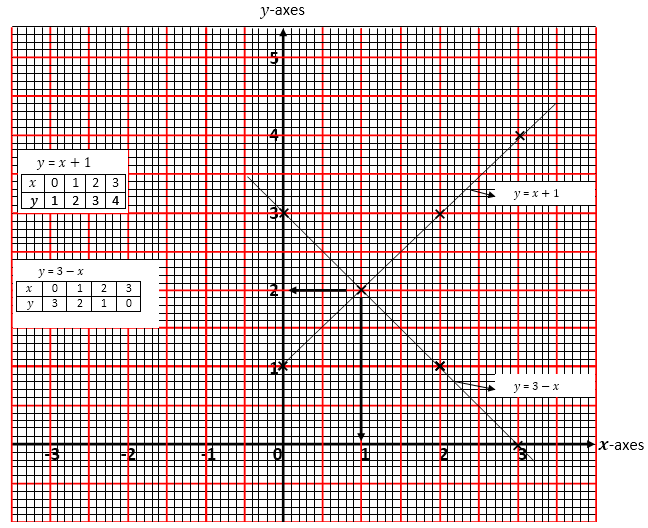
The two lines intersect at the coordinates (1,2)
i.e x=1,y=2.
Therefore x=1,y=2 is the solution of the simultaneous equations
x-y=-1 and x+y=3
Example 2.
Solve graphically the simultaneous equations
2x-y= -1 and x-2y=4 for -1 ≤ x ≤ 3
Solution
Considering equation 2x-y=-1,
We make y the subject of the formula
Thus, y=2x+1
When x=-1, y=2(-1)+1=-2+1=-1
When x=0, y=2(0)+1=0+1=1
When x=1, y=2(1)+1=2+1=3
When x=2, y=2(2)+1=4+1=5
When x=3, y=2(3)+1=6+1=7
Similarly, considering equation x-2y=4,
Using a scale of 1cm = 1unit on y-axes and 2cm = 1unit on x-axes, we plot a graph of y against x for the two equations as shown in the graph below.
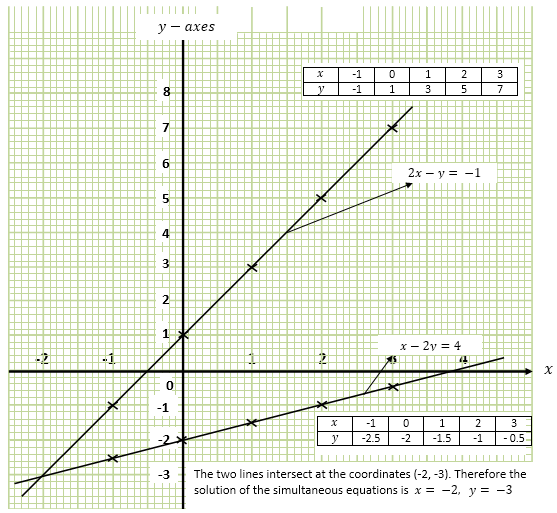
Example 3.
Solve graphically 3x+2y=4………………….1 for -2 ≤ x ≤ 1
2x+3y=1…………………..2
Solution:
Considering the equation, 3x+2y=4,
We make y the subject of the formula.
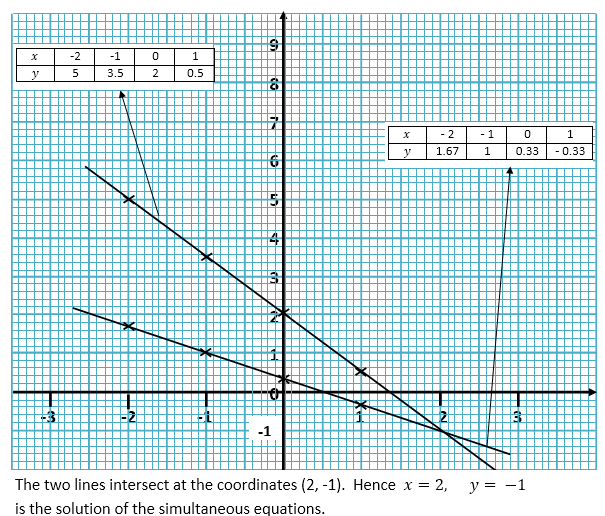
ASSIGNMENT:
Nelson Functional Mathematics for Junior Secondary Schools, Book 3. Page 87. Questions 1-5.
READING ASSIGNMENT:
New General Mathematics for West Africa, for junior secondary school, U.B.E Edition Book 3). Pages 133 – 136
Topic: Solving simultaneous equations using method by substitution and method by elimination.
Content: i. Method by substitution
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Graphical Method
OBJECTIVES: At the end of the lesson, the students should be able to:
Construct tables of values.
CONTENT:
Simultaneous Equation (Graphical method)
Example 1: Construct table of value for the equation below.
Y =3x-3 for values of x from -3 to +3
Solution
Construct table of values for equation 1& 2 for values of x from -3 to +3
x -3 -2 -1 0 1 2 3
3x -9 -6 -3 0 3 6 9
-3 -3 -3 -3 -3 -3 -3 -3
y -12 -9 -6 -3 0 3 6
http://www.slideshare.net/MoreThanMaths ... ons-519735
EVALUATION: Construct table of values for the following equations.
(1) x + 3y = 6 ...................(1)
3x +y = -10............... (2)
(2) 3x + 2y = 15 ...................(1)
2x - y = 7................. (2)
ASSIGNMENT:
(1) 3x -y =6...............(1)
2x -4y =14................ (2)
(2) 3x -2y =6 ...............(1)
2x -5y =-4............. (2)
further studies
http://www.mathsteacher.com.au/year10/c ... lution.htm
practice test
http://www.scruffs.shetland.co.uk/files/simgraph2.htm
watch video
http://www.mathexpression.com/y-intercept.html
LESSON 44
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Graphical Method
OBJECTIVE: At the end of the lesson, the students should be able to:
Solve some problems on simultaneous equations by Elimination method.
CONTENT:
Simultaneous Equation
Example 1: Solve the equation by Graphical method, If the value of x =-3 to +3
8X + Y = 13 ............... (1)
Solution
y =13 -8x
x -3 -2 -1 0 1 2 3
-8x +24 +16 +8 0 -8 -16 -24
13 13 13 13 13 13 13 13
Y +37 +29 +21 +13 +5 -3 -11
EVALUATION: Solve the following problems using Elimination method.
2 x +y = 18 ...................(1)
3x - y = 12................ .... (2)
2x - y = 14................... ...(1)
x +y = 10................... ..(2)
ASSIGNMENT:
(1) 2y+-y =24.................(1)
4x - y =12............... (2)
(2) 4x - y =-13 ................(1)
3x +y =17.................. (2)
further studies
http://www.teacherschoice.com.au/Maths_ ... Alg_11.htm
practice test
http://hsmathangcc.wiki.hci.edu.sg/Simu ... +Equations
watch video
[youtube]https://youtu.be/OFhIqZg8G0w[/youtube]
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Graphical Method
OBJECTIVE: At the end of the lesson, the students should be able to:
Compute two equations at a time.
CONTENT:
SIMULTANEOUS EQUATION(GRAPHICAL METHOD)
Example 1: Construct the tables of values for the equation below.
5X + Y = 12 ............ (1)
x -y = 6 .................(2)
Solution
Y = 12-5x.................... (1)
x -3 -2 -1 0 1 2 3
-5x +15 +10 +5 0 -5 -10 -15
12 12 12 12 12 12 12 12
y +27 +22 +17 +12 +7 +2 -3
Y = -6+x
x -3 -2 -1 0 1 2 3
-6 -6 -6 -6 -6 -6 -6 -6
x -3 -2 -1 0 1 2 3
y -9 -8 -7 -6 -5 -4 -3
Combine the two equations together, we have
x -3 -2 -1 0 1 2 3
Y1 +27 +22 +17 +12 +7 +2 -3
Y2 -9 -8 -7 -6 -5 -4 -3
EVALUATION: Construct tables of values for the following problems.
(1) 2x - y = 27 ...................(1)
3x + y = 13................ (2)
(2) 3x +y =16................... (1)
2x - y = 10................. (2)
ASSIGNMENT:
(1) 3x -y =-23.................(1)
2 x +y =-11 ...............(2)
(2) 3x - y = 20 ...............(1)
2x + y =14 ................(2)
further studies
http://www.webmath.com/solver2.html
http://www.bbc.co.uk/schools/gcsebitesi ... rev1.shtml
practice test
http://www.platinumgmat.com/gmat_study_ ... _equations
watch video
[youtube]https://youtu.be/KeP2QQgXQB0[/youtube]
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Graphical Method
OBJECTIVE: At the end of the lesson, the students should be able to:
Solve some problems on simultaneous equations by Graphical method.
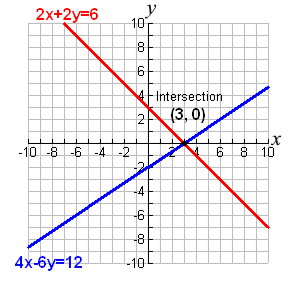
CONTENT:
SIMULTANEOUS EQUATION (GRAPHICAL METHOD)
Example 1: Solve the system of equation by elimination method
3x+4y = 10 ............. ....(1)
2x+y =5 ................ (2)
Solution
Y = 10 -3x/4
x -3 -2 -1 0 1 2 3
-3x +9 +6 +3 0 -3 -6 -9
10 10 10 10 -6 10 10 10
y 4.75 4 3.25 2.5 1.75 1 0.25
Y = 5-2x
x -3 -2 -1 0 1 2 3
-2x +6 +4 +2 0 -2 -4 -6
5 5 5 5 5 5 5 5
y 11 9 7 5 3 1 -1
Combine the two equations together
x -3 -2 -1 0 1 2 3
Y1 4.75 4 3.25 2.5 1.75 1 0.25
Y2 11 9 7 5 3 1 -1
See the graph of the equation below;
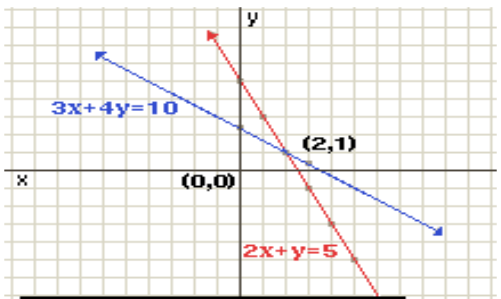
X =2 & y = 1
EVALUATION: solve the following problems using graphical method.
(1) x-y =1 ...................(1)
X + y = 3 ................ (2)
(2) x +y = 10 ................... (1)
Y= x+4 ................. (2)
ASSIGNMENT:
x- 1/4y =2 .................(1)
x - 3/4y =2................ (2)
further studies
http://www.revisionworld.co.uk/gcse-rev ... ear-graphs
watch video
[youtube]http://www.youtube.com/watch?v=MFfWfu6Q76A[/youtube]
[youtube]http://www.youtube.com/watch?v=VymyU4Ksgrc[/youtube]
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Graphical Method
OBJECTIVE: At the end of the lesson, the students should be able to:
Solve some problems on simultaneous equations by Graphical method.
CONTENT:
SIMULTANEOUS EQUATION
Example 1: Solve the system of equation by both substitution and Graphical method.
x-y = 6 ............. ....(1)
2x+y =3 ................ (2)
Solution
Y = x-6
x -3 -2 -1 0 1 2 3
x -3 -2 -1 0 1 2 3
-6 -6 -6 -6 -6 -6 -6 -6
y -9 -8 -7 -6 -6 -4 -3
Y = 3-2x
x -3 -2 -1 0 1 2 3
-2x +6 +4 +2 0 -2 -4 -6
3 3 3 3 3 3 3 3
y 9 7 5 3 1 -1 -3
Combine the two equations together
x -3 -2 -1 0 1 2 3
Y1 -9 -8 -7 -6 -6 -4 -3
Y2 +9 +7 +5 +3 +1 -1 -3
Attempt a graph of the equation above
http://www.webgraphing.com/plotting_bas ... fAodhCaELQ
EVALUATION: The lesson is evaluated as the students are asked to solve the following problems using both substitution and Elimination method.
(1) x + 2y = 15 ...................(1)
3x - y = 6............... (2)
(2) x + 2y = 7 ...................(1)
3x - 4y =4................. (2)
ASSIGNMENT:
(1) 3x -2y =4...............(1)
X -4y =8................ (2)
(2) 2x - y =1 ...............(1)
2x -5y =-1............. (2)
further studies
http://regentsprep.org/Regents/math/ALG ... /GrSys.htm
watch video
[youtube]http://www.youtube.com/watch?v=MFfWfu6Q76A[/youtube]
CONTENT:
Concept of simultaneous equations
Preparing table of values for variables
Graphical approach to the solution of simultaneous equations
SUB TOPIC: CONCEPT OF SIMULTANEOUS EQUATIONS
Equations such as
x-y= -1……………………..i
x+y=3……………………...ii
With two variables x and y to be solved at the same time are called simultaneous equations.
SUB TOPIC: PREPARING TABLE OF VALUES.
The above equations x-y= -1,x+y=3 are both linear equations with two variables. For a certain value of x, y has a corresponding value. For example, considering the equation x-y= -1, making y the subject of the formula,
y = x + 1.
When x takes the value 0, y=0+1=1, When x takes the value 1, y=1+1=2. When x takes the value 2, y=2+1=3. When x takes the value 3, y=3+1=4. The result can be displayed in a table as shown below
The table above is known as table of specification. The table can be extended if we assign more values to x
EVALUATION
a. Prepare table of specification for the equation y=3-x for x=0 to 2
b. Copy and complete the table for the relation y=[sup]1[/sup]/[sub]2[/sub] + x
SUB TOPIC: GRAPHICAL METHOD OF SOLVING SIMULTANEOUS EQUATIONS
This method involves creating tables of values for both variables or unknowns. y is usually made the subject of the formula and referred to as the dependent variable while x is the independent variable. Simple values can be assigned to x in order to determine the corresponding values of y. Although two plotted points are enough to draw the lines of both equations, it is advisable to plot at least three points. After plotting, the points are expected to lie on the same straight line for both equations. The lines should intersect at a point or this can be achieved by extending one or both lines with a ruler. The point of intersection of the lines gives the solutions of the simultaneous equations. If the lines are parallel, it means the simultaneous equations have no solution.
Example 1
Solve using graphical approach:
x-y= -1……………………..i
x+y=3………………………...ii
Solution
We assign four values to x (0, 1, 2 and 3) and use them to find the corresponding values of y for both equations.
Considering equation 1 (y=x+1).
When x = 0, y = 0 +1 = 1.
When x = 1, y = 1 + 1 = 2.
When x = 2, y = 2 + 1 = 3.
When x = 3, y = 3 +1 = 4.
y = x+1
x 0 1 2 3
y 1 2 3 4
Similarly, from equation ii,
y = 3 – x.
When x = 0, y = 3 – 0 = 3.
When x = 1, y=3-1=2.
When x = 2, y=3-2=1.
When x=3, y=3-3=0
y = 3-x
x 0 1 2 3
y 3 2 1 0
Using a scale of 2cm = 1 unit for both axes, we plot a graph of y against x for both equations. See the graph below
The two lines intersect at the coordinates (1,2)
i.e x=1,y=2.
Therefore x=1,y=2 is the solution of the simultaneous equations
x-y=-1 and x+y=3
Example 2.
Solve graphically the simultaneous equations
2x-y= -1 and x-2y=4 for -1 ≤ x ≤ 3
Solution
Considering equation 2x-y=-1,
We make y the subject of the formula
Thus, y=2x+1
When x=-1, y=2(-1)+1=-2+1=-1
When x=0, y=2(0)+1=0+1=1
When x=1, y=2(1)+1=2+1=3
When x=2, y=2(2)+1=4+1=5
When x=3, y=2(3)+1=6+1=7
Similarly, considering equation x-2y=4,
Using a scale of 1cm = 1unit on y-axes and 2cm = 1unit on x-axes, we plot a graph of y against x for the two equations as shown in the graph below.
Example 3.
Solve graphically 3x+2y=4………………….1 for -2 ≤ x ≤ 1
2x+3y=1…………………..2
Solution:
Considering the equation, 3x+2y=4,
We make y the subject of the formula.
ASSIGNMENT:
Nelson Functional Mathematics for Junior Secondary Schools, Book 3. Page 87. Questions 1-5.
READING ASSIGNMENT:
New General Mathematics for West Africa, for junior secondary school, U.B.E Edition Book 3). Pages 133 – 136
Topic: Solving simultaneous equations using method by substitution and method by elimination.
Content: i. Method by substitution
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Graphical Method
OBJECTIVES: At the end of the lesson, the students should be able to:
Construct tables of values.
CONTENT:
Simultaneous Equation (Graphical method)
Example 1: Construct table of value for the equation below.
Y =3x-3 for values of x from -3 to +3
Solution
Construct table of values for equation 1& 2 for values of x from -3 to +3
x -3 -2 -1 0 1 2 3
3x -9 -6 -3 0 3 6 9
-3 -3 -3 -3 -3 -3 -3 -3
y -12 -9 -6 -3 0 3 6
http://www.slideshare.net/MoreThanMaths ... ons-519735
EVALUATION: Construct table of values for the following equations.
(1) x + 3y = 6 ...................(1)
3x +y = -10............... (2)
(2) 3x + 2y = 15 ...................(1)
2x - y = 7................. (2)
ASSIGNMENT:
(1) 3x -y =6...............(1)
2x -4y =14................ (2)
(2) 3x -2y =6 ...............(1)
2x -5y =-4............. (2)
further studies
http://www.mathsteacher.com.au/year10/c ... lution.htm
practice test
http://www.scruffs.shetland.co.uk/files/simgraph2.htm
watch video
http://www.mathexpression.com/y-intercept.html
LESSON 44
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Graphical Method
OBJECTIVE: At the end of the lesson, the students should be able to:
Solve some problems on simultaneous equations by Elimination method.
CONTENT:
Simultaneous Equation
Example 1: Solve the equation by Graphical method, If the value of x =-3 to +3
8X + Y = 13 ............... (1)
Solution
y =13 -8x
x -3 -2 -1 0 1 2 3
-8x +24 +16 +8 0 -8 -16 -24
13 13 13 13 13 13 13 13
Y +37 +29 +21 +13 +5 -3 -11
EVALUATION: Solve the following problems using Elimination method.
2 x +y = 18 ...................(1)
3x - y = 12................ .... (2)
2x - y = 14................... ...(1)
x +y = 10................... ..(2)
ASSIGNMENT:
(1) 2y+-y =24.................(1)
4x - y =12............... (2)
(2) 4x - y =-13 ................(1)
3x +y =17.................. (2)
further studies
http://www.teacherschoice.com.au/Maths_ ... Alg_11.htm
practice test
http://hsmathangcc.wiki.hci.edu.sg/Simu ... +Equations
watch video
[youtube]https://youtu.be/OFhIqZg8G0w[/youtube]
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Graphical Method
OBJECTIVE: At the end of the lesson, the students should be able to:
Compute two equations at a time.
CONTENT:
SIMULTANEOUS EQUATION(GRAPHICAL METHOD)
Example 1: Construct the tables of values for the equation below.
5X + Y = 12 ............ (1)
x -y = 6 .................(2)
Solution
Y = 12-5x.................... (1)
x -3 -2 -1 0 1 2 3
-5x +15 +10 +5 0 -5 -10 -15
12 12 12 12 12 12 12 12
y +27 +22 +17 +12 +7 +2 -3
Y = -6+x
x -3 -2 -1 0 1 2 3
-6 -6 -6 -6 -6 -6 -6 -6
x -3 -2 -1 0 1 2 3
y -9 -8 -7 -6 -5 -4 -3
Combine the two equations together, we have
x -3 -2 -1 0 1 2 3
Y1 +27 +22 +17 +12 +7 +2 -3
Y2 -9 -8 -7 -6 -5 -4 -3
EVALUATION: Construct tables of values for the following problems.
(1) 2x - y = 27 ...................(1)
3x + y = 13................ (2)
(2) 3x +y =16................... (1)
2x - y = 10................. (2)
ASSIGNMENT:
(1) 3x -y =-23.................(1)
2 x +y =-11 ...............(2)
(2) 3x - y = 20 ...............(1)
2x + y =14 ................(2)
further studies
http://www.webmath.com/solver2.html
http://www.bbc.co.uk/schools/gcsebitesi ... rev1.shtml
practice test
http://www.platinumgmat.com/gmat_study_ ... _equations
watch video
[youtube]https://youtu.be/KeP2QQgXQB0[/youtube]
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Graphical Method
OBJECTIVE: At the end of the lesson, the students should be able to:
Solve some problems on simultaneous equations by Graphical method.
CONTENT:
SIMULTANEOUS EQUATION (GRAPHICAL METHOD)
Example 1: Solve the system of equation by elimination method
3x+4y = 10 ............. ....(1)
2x+y =5 ................ (2)
Solution
Y = 10 -3x/4
x -3 -2 -1 0 1 2 3
-3x +9 +6 +3 0 -3 -6 -9
10 10 10 10 -6 10 10 10
y 4.75 4 3.25 2.5 1.75 1 0.25
Y = 5-2x
x -3 -2 -1 0 1 2 3
-2x +6 +4 +2 0 -2 -4 -6
5 5 5 5 5 5 5 5
y 11 9 7 5 3 1 -1
Combine the two equations together
x -3 -2 -1 0 1 2 3
Y1 4.75 4 3.25 2.5 1.75 1 0.25
Y2 11 9 7 5 3 1 -1
See the graph of the equation below;
X =2 & y = 1
EVALUATION: solve the following problems using graphical method.
(1) x-y =1 ...................(1)
X + y = 3 ................ (2)
(2) x +y = 10 ................... (1)
Y= x+4 ................. (2)
ASSIGNMENT:
x- 1/4y =2 .................(1)
x - 3/4y =2................ (2)
further studies
http://www.revisionworld.co.uk/gcse-rev ... ear-graphs
watch video
[youtube]http://www.youtube.com/watch?v=MFfWfu6Q76A[/youtube]
[youtube]http://www.youtube.com/watch?v=VymyU4Ksgrc[/youtube]
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Graphical Method
OBJECTIVE: At the end of the lesson, the students should be able to:
Solve some problems on simultaneous equations by Graphical method.
CONTENT:
SIMULTANEOUS EQUATION
Example 1: Solve the system of equation by both substitution and Graphical method.
x-y = 6 ............. ....(1)
2x+y =3 ................ (2)
Solution
Y = x-6
x -3 -2 -1 0 1 2 3
x -3 -2 -1 0 1 2 3
-6 -6 -6 -6 -6 -6 -6 -6
y -9 -8 -7 -6 -6 -4 -3
Y = 3-2x
x -3 -2 -1 0 1 2 3
-2x +6 +4 +2 0 -2 -4 -6
3 3 3 3 3 3 3 3
y 9 7 5 3 1 -1 -3
Combine the two equations together
x -3 -2 -1 0 1 2 3
Y1 -9 -8 -7 -6 -6 -4 -3
Y2 +9 +7 +5 +3 +1 -1 -3
Attempt a graph of the equation above
http://www.webgraphing.com/plotting_bas ... fAodhCaELQ
EVALUATION: The lesson is evaluated as the students are asked to solve the following problems using both substitution and Elimination method.
(1) x + 2y = 15 ...................(1)
3x - y = 6............... (2)
(2) x + 2y = 7 ...................(1)
3x - 4y =4................. (2)
ASSIGNMENT:
(1) 3x -2y =4...............(1)
X -4y =8................ (2)
(2) 2x - y =1 ...............(1)
2x -5y =-1............. (2)
further studies
http://regentsprep.org/Regents/math/ALG ... /GrSys.htm
watch video
[youtube]http://www.youtube.com/watch?v=MFfWfu6Q76A[/youtube]
WEEK 3
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Elimination Method
OBJECTIVE: At the end of the lesson, the students should be able to:
Solve some problems on simultaneous equations by elimination method.
CONTENT:
SIMULTANEOUS EQUATION (ELIMINATION METHOD)
Example 1: Solve the system of equation by elimination ion method
5X + 3Y = 12 ............(1)
x -3y = 6 .................(2)
Solution
Adding equations 1 & 2 gives
(5x + 3y) + (x - 3y) = 12 + 6
5x +x +3y -3y = 18
6x = 18
X = 3
Substitute this value of x in equation 2
X -3y = 6
3 -3y = 6
-3y = 6 - 3 = 3
Y = -3/3
Therefore Y = -1
EVALUATION: solve the following problems using elimination method.
(1) 2 x +3y = 7 ...................(1)
4x + 3y = 11................ (2)
(2) x +2 y = 6 ................... (1)
3x - y =- 10................. (2)
ASSIGNMENT:
(1) 3x -y =-3.................(1)
x +y =-1 ...............(2)
(2) 3x - y = 21 ...............(1)
2x + y =4 ................(2)
further studies
http://www.mathsteacher.com.au/year10/c ... d/elim.htm
practice test
http://www.skwirk.com/p-c_s-12_u-63_t-1 ... -equations
watch video
[youtube]http://www.youtube.com/watch?v=XM7Q4Oj5OTc[/youtube]
[youtube]http://www.youtube.com/watch?v=BezAEABVgOI[/youtube]
LESSON 40
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Elimination Method
OBJECTIVE: At the end of the lesson, the students should be able to:
Solve some problems on simultaneous equations by elimination method.
CONTENT:
SIMULTANEOUS EQUATION (ELIMINATION METHOD)
Example 1: Solve the system of equation by elimination method
x+ 2y = 6 ............. ....(1)
3x -y =-10 ................ (2)
Solution
Multiply equation 1 by 1, we obtain an equivalent equation.
x + 2y = 6 ................ (3)
Multiply equation 2 by 2, we obtain equivalent equation
6x -2y = -20.............. (4)
Add equations 3 and 4, we obtain
(x + 2y) + (6x -2y) =6 +(-20) = 6 - 20
X + 6x +2y -2y = -14
7x = -14
X =-2
Substitute this value of x in equation 1
X + 2y =6
-2 +2y =6
2y = 6 +2
2y = 8
Y= 4
EVALUATION:
(1) 4a =5 + 2b ...................(1)
6b = 9 - 4a................ (2)
(2) x +3y = 6 ................... (1)
4x +3y = 9................. (2)
ASSIGNMENT:
(1) 3x +y =9.................(1)
2y -x =4................ (2)
(3) x +y =10 ................(1)
x -y =-2.................. (2)
further studies
http://catman3000.hubpages.com/hub/Solv ... ion-method
http://www.teacherschoice.com.au/maths_ ... alg_10.htm
practice test
http://sec3ithomelearning.wetpaint.com/ ... s+Equation
watch video
[youtube]http://www.youtube.com/watch?v=PgARVIawA5U[/youtube]
[youtube]http://www.youtube.com/watch?v=xee7Qqqd ... re=channel[/youtube]
[youtube]http://www.youtube.com/watch?v=O-rrOPPm ... re=channel[/youtube]
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Substitution and Elimination Method
OBJECTIVE: At the end of the lesson, the students should be able to:
Solve some problems on simultaneous equations by substitution method.
CONTENT:
SIMULTANEOUS EQUATION
Example 1: Solve the system of equation by both substitution and Elimination method
x - y = 3............. (1)
2x + 3y = 16................. (2)
Solution
Step 1
Solve one of the equations for one of its variables.
From equation (1), we solve for x
X =3 + y
Step 2
Substitute that quantity for the same variable in the other equation. In equation (2) we substitute for x.
2(3 + y) + 3y =16
6 + 2y + 3y = 16
Hence: 5y = 16 - 6
5y = 10
Y =2
To find x, substitute 2 for y in the equation.
X = 3 + y, that
X = 3 +2 =5
Therefore; x = 5
Or, x - y = 3................(1)
2x +3y = 16...........(2)
Multiply equation 1 by 2 and equation 2 by 1
Hence, we have 2x - 2y =6..........(3)
2x + 3y =16....... (4)
Subtract equation 3 from equation 4
5y =10
Y =2
Then substitute for y in equation 1
X -2 =3
X =3 +2
X = 5
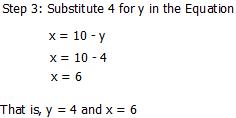
EVALUATION: The lesson is evaluated as the students are asked to solve the following problems using both substitution and Elimination method.
(1) x + 2y = 6 ...................(1)
3x - y = -10............... (2)
(2) x + 2y = 9 ...................(1)
3x - 4y = 7................. (2)
ASSIGNMENT:
(1) 3x -2y =4...............(1)
X -4y =8................ (2)
(2) 2x - y =1 ...............(1)
2x -5y =-1............. (2)
further studies
http://www.gcseguide.co.uk/simultaneous_equations.htm
http://math.tutorvista.com/algebra/simu ... tions.html
practice test
http://www.skwirk.com.au/p-c_s-12_u-63_ ... -equations
watch video
[youtube]http://www.youtube.com/watch?v=71VuWNfR8MU[/youtube]
http://burgermath.mindbites.com/lesson/ ... limination
SPECIFIC TOPIC: Elimination Method
OBJECTIVE: At the end of the lesson, the students should be able to:
Solve some problems on simultaneous equations by elimination method.
CONTENT:
SIMULTANEOUS EQUATION (ELIMINATION METHOD)
Example 1: Solve the system of equation by elimination ion method
5X + 3Y = 12 ............(1)
x -3y = 6 .................(2)
Solution
Adding equations 1 & 2 gives
(5x + 3y) + (x - 3y) = 12 + 6
5x +x +3y -3y = 18
6x = 18
X = 3
Substitute this value of x in equation 2
X -3y = 6
3 -3y = 6
-3y = 6 - 3 = 3
Y = -3/3
Therefore Y = -1
EVALUATION: solve the following problems using elimination method.
(1) 2 x +3y = 7 ...................(1)
4x + 3y = 11................ (2)
(2) x +2 y = 6 ................... (1)
3x - y =- 10................. (2)
ASSIGNMENT:
(1) 3x -y =-3.................(1)
x +y =-1 ...............(2)
(2) 3x - y = 21 ...............(1)
2x + y =4 ................(2)
further studies
http://www.mathsteacher.com.au/year10/c ... d/elim.htm
practice test
http://www.skwirk.com/p-c_s-12_u-63_t-1 ... -equations
watch video
[youtube]http://www.youtube.com/watch?v=XM7Q4Oj5OTc[/youtube]
[youtube]http://www.youtube.com/watch?v=BezAEABVgOI[/youtube]
LESSON 40
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Elimination Method
OBJECTIVE: At the end of the lesson, the students should be able to:
Solve some problems on simultaneous equations by elimination method.
CONTENT:
SIMULTANEOUS EQUATION (ELIMINATION METHOD)
Example 1: Solve the system of equation by elimination method
x+ 2y = 6 ............. ....(1)
3x -y =-10 ................ (2)
Solution
Multiply equation 1 by 1, we obtain an equivalent equation.
x + 2y = 6 ................ (3)
Multiply equation 2 by 2, we obtain equivalent equation
6x -2y = -20.............. (4)
Add equations 3 and 4, we obtain
(x + 2y) + (6x -2y) =6 +(-20) = 6 - 20
X + 6x +2y -2y = -14
7x = -14
X =-2
Substitute this value of x in equation 1
X + 2y =6
-2 +2y =6
2y = 6 +2
2y = 8
Y= 4
EVALUATION:
(1) 4a =5 + 2b ...................(1)
6b = 9 - 4a................ (2)
(2) x +3y = 6 ................... (1)
4x +3y = 9................. (2)
ASSIGNMENT:
(1) 3x +y =9.................(1)
2y -x =4................ (2)
(3) x +y =10 ................(1)
x -y =-2.................. (2)
further studies
http://catman3000.hubpages.com/hub/Solv ... ion-method
http://www.teacherschoice.com.au/maths_ ... alg_10.htm
practice test
http://sec3ithomelearning.wetpaint.com/ ... s+Equation
watch video
[youtube]http://www.youtube.com/watch?v=PgARVIawA5U[/youtube]
[youtube]http://www.youtube.com/watch?v=xee7Qqqd ... re=channel[/youtube]
[youtube]http://www.youtube.com/watch?v=O-rrOPPm ... re=channel[/youtube]
MAIN TOPIC: Simultaneous Equation
SPECIFIC TOPIC: Substitution and Elimination Method
OBJECTIVE: At the end of the lesson, the students should be able to:
Solve some problems on simultaneous equations by substitution method.
CONTENT:
SIMULTANEOUS EQUATION
Example 1: Solve the system of equation by both substitution and Elimination method
x - y = 3............. (1)
2x + 3y = 16................. (2)
Solution
Step 1
Solve one of the equations for one of its variables.
From equation (1), we solve for x
X =3 + y
Step 2
Substitute that quantity for the same variable in the other equation. In equation (2) we substitute for x.
2(3 + y) + 3y =16
6 + 2y + 3y = 16
Hence: 5y = 16 - 6
5y = 10
Y =2
To find x, substitute 2 for y in the equation.
X = 3 + y, that
X = 3 +2 =5
Therefore; x = 5
Or, x - y = 3................(1)
2x +3y = 16...........(2)
Multiply equation 1 by 2 and equation 2 by 1
Hence, we have 2x - 2y =6..........(3)
2x + 3y =16....... (4)
Subtract equation 3 from equation 4
5y =10
Y =2
Then substitute for y in equation 1
X -2 =3
X =3 +2
X = 5
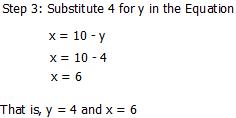
EVALUATION: The lesson is evaluated as the students are asked to solve the following problems using both substitution and Elimination method.
(1) x + 2y = 6 ...................(1)
3x - y = -10............... (2)
(2) x + 2y = 9 ...................(1)
3x - 4y = 7................. (2)
ASSIGNMENT:
(1) 3x -2y =4...............(1)
X -4y =8................ (2)
(2) 2x - y =1 ...............(1)
2x -5y =-1............. (2)
further studies
http://www.gcseguide.co.uk/simultaneous_equations.htm
http://math.tutorvista.com/algebra/simu ... tions.html
practice test
http://www.skwirk.com.au/p-c_s-12_u-63_ ... -equations
watch video
[youtube]http://www.youtube.com/watch?v=71VuWNfR8MU[/youtube]
http://burgermath.mindbites.com/lesson/ ... limination
WEEK 4
TOPIC: SOLVING SIMULTANEOUS EQUATIONS USING METHOD BY SUBSTITUTION AND BY ELIMINATION
CONTENT:
I. METHOD BY SUBSTITUTION
II. METHOD BY ELIMINATION
SUB TOPIC: METHOD BY SUBSTITUTION.
This is a method in which one variable is made the subject of the formula and substituted in the second equation. This will lead to a third equation with one variable. The equation is then solved for the value of the variable. This value can be substituted in any of the first two equations for the value of the second variable. See examples below.
Example 1.
Solve 2x+y=4……………..1
3x-y= -1[sup]1[/sup]/[sub]2[/sub] ……….2
using method by substitution
Solution
Example 2
Solve 3x-4y= - 6……………………………………..1
7x-2y=8………………………………………….2
Using method by substitution.
Solution
3x-4y=- 6 …………………………………………………………………eqn 1
7x-2y=8……………………………………………………………………..eqn 2
Now, put y=3 into eqn1
Thus, 3x-4(3)=- 6
3x-12=-6
Or 3x=12-6
3x=6
Thus, x=[sup]6[/sup]/[sub]3[/sub] = 2
Hence x=2,y=3 is the solution of the simultaneous equations
Check: 3(2)-4(3)=6-12=- 6……………………………………………eqn 1
7(2)-2(3)=14-6=8……………………………………………………….….eqn 2
EVALUATION
Using method by substitution, solve x-y=0, y-3x=1
METHOD BY ELIMINATION
Example 4
Solve 7x-2y=8……………………………………………………….1
3x-4y=-6…………………………………………………..…2
Solution:
Multiply eqn 1 by 4 and eqn 2 by 2
7x-2y=8………………………………eqn 1 x 4
3x-4y=-6……………………………eqn 2 x 2
4×7x-4×2y=8×4……………………….1
2×3x-2×4y=-6×2…………………….2
28x-8y=32………………………………………..1
6x-8y=-12………………………………..……..2
EVALUATION
Solve the equations 3x+2y=7, 4x-2y=7 using method by elimination
ASSIGNMENT
(a) Solve the equation [sup](p-5q)[/sup]/[sub]2[/sub] = p-3, 5p-10q=16 simultaneously using any method of your choice
(b) Solve 2x+3y-1=3, 2x-2y=2 Using method by graph, method by elimination and method by substitution
READING ASSIGNMENT
Nelson Functional Mathematics for Junior Secondary school, book 3 Pg 87 – 91.
TOPIC: SIMILAR FIGURES AND ENLARGEMENT
CONTENT:
i. Concept of similar figures
ii. Examples of similar figures
iii. Enlargement and scale factor
SUB TOPIC: CONCEPT OF SIMILAR FIGURES
Two figures are similar, if they look alike and one is an enlargement or reduction of the other. Mathematically, if two shapes are similar, the ratio of their corresponding sides should be constant.
EXAMPLES OF SIMILAR FIGURES
(a) Similar photographs
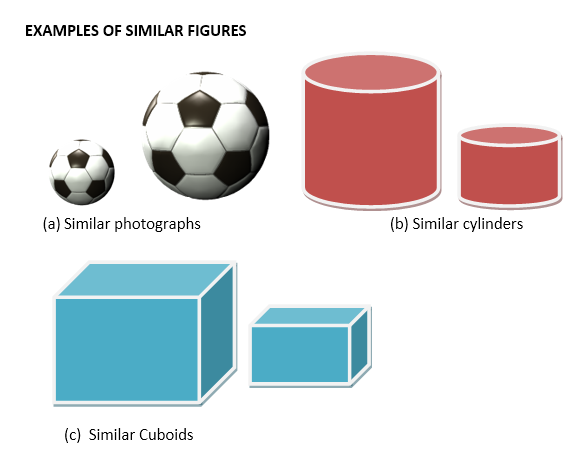
Look at the photographs above. Although each of the two photographs are not of the same size, they look alike. We say that the pictures are similar to each other.
ENLARGEMENT AND SCALE FACTOR
The photograph in fig. a above is enlarged such that the sides are proportional. In this case, the ratio of the corresponding sides will be constant. Look at the example below.
Example 1
(a) Measure the length and breadth of the picture in fig. (a)
(b) Find the ratio length : breadth
(c) What do you notice?
Solution
(a) Length = 2cm, Breadth = 4cm (smaller picture)
Length = 2.4cm Breadth = 4.8cm (larger picture)
(b) Length :breadth = 4 : 2 = [sup]4[/sup]/[sub]2[/sub] = 2 (smaller picture)
Length : breadth = 4.8 : 2.4 = [sup]4.8[/sup]/[sub]2.4[/sub] = 2 (larger picture)
(c) The ratio of length to breadth for each picture is 2
Length : breadth is constant for both pictures in (a) this means that the first picture is an enlargement of the second picture. Hence when a shape is reduced or enlarged to give another shape such that the ratio of their corresponding sides are the same, we say, the two shapes are similar mathematically. This ratio is what we call the scale factor. The scale factor for the pictures in (a) is 2
Example 2
Consider the shapes below and indicate whether they are similar or not
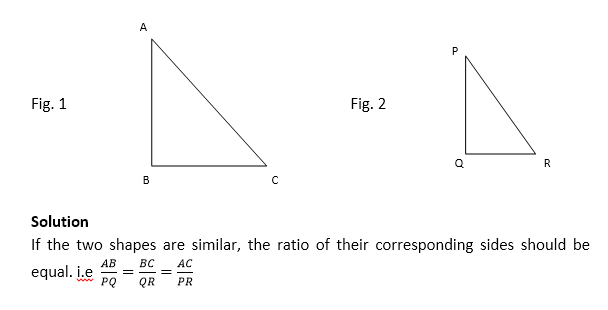
Considering Fig. 1,
AB = 3.2cm
BC = 2.9cm
AC = 4.3cm
Similarly, in fig. 2,
PQ = 2.4cm
QR = 1.8cm
PR = 3.0cm
( AB)/PQ=[sup]3.2[/sup]/[sub]2.4[/sub] = 1.33
BC/QR=[sup]2.9[/sup]/[sub]1.8[/sub] = 1.61
AC/PR=[sup]4.2[/sup]/[sub]3.0[/sub] = 1.40
From the above calculations, it is clear that the ratios of the corresponding sides are not equal i.e AB/PQ≠BC/QR≠AC/PR. We therefore conclude that the two triangles are not similar.
QUESTIONS.
State whether the following statements are true or false
i. Two figures are similar, if one is a reduction of the other
ii. Two figures are not similar, if one is an enlargement of the other
iii. All isosceles triangles are similar
iv. All cuboids are similar
v. All pictures or images in the television are similar to the original bodies
vi All cubes are similar
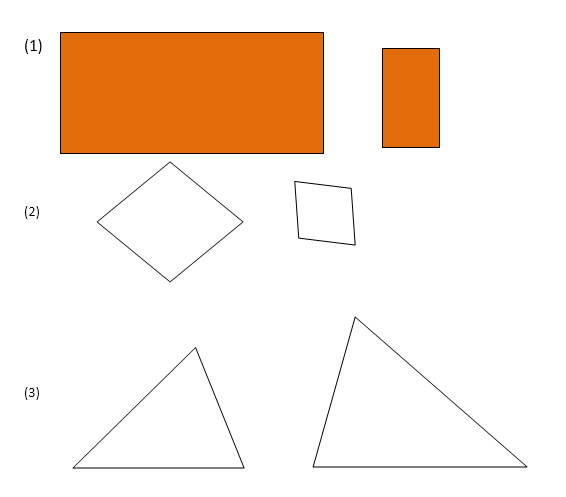
EVALUATION
Consider the following shapes and indicate whether they are similar or not. Use measurement if you are not sure.
ASSIGNMENT
(Work book, Nelson Functional Mathematics for Junior secondary school, book 3). Page 44 and 45. Exercise A
CONTENT:
I. METHOD BY SUBSTITUTION
II. METHOD BY ELIMINATION
SUB TOPIC: METHOD BY SUBSTITUTION.
This is a method in which one variable is made the subject of the formula and substituted in the second equation. This will lead to a third equation with one variable. The equation is then solved for the value of the variable. This value can be substituted in any of the first two equations for the value of the second variable. See examples below.
Example 1.
Solve 2x+y=4……………..1
3x-y= -1[sup]1[/sup]/[sub]2[/sub] ……….2
using method by substitution
Solution
Example 2
Solve 3x-4y= - 6……………………………………..1
7x-2y=8………………………………………….2
Using method by substitution.
Solution
3x-4y=- 6 …………………………………………………………………eqn 1
7x-2y=8……………………………………………………………………..eqn 2
Now, put y=3 into eqn1
Thus, 3x-4(3)=- 6
3x-12=-6
Or 3x=12-6
3x=6
Thus, x=[sup]6[/sup]/[sub]3[/sub] = 2
Hence x=2,y=3 is the solution of the simultaneous equations
Check: 3(2)-4(3)=6-12=- 6……………………………………………eqn 1
7(2)-2(3)=14-6=8……………………………………………………….….eqn 2
EVALUATION
Using method by substitution, solve x-y=0, y-3x=1
METHOD BY ELIMINATION
Example 4
Solve 7x-2y=8……………………………………………………….1
3x-4y=-6…………………………………………………..…2
Solution:
Multiply eqn 1 by 4 and eqn 2 by 2
7x-2y=8………………………………eqn 1 x 4
3x-4y=-6……………………………eqn 2 x 2
4×7x-4×2y=8×4……………………….1
2×3x-2×4y=-6×2…………………….2
28x-8y=32………………………………………..1
6x-8y=-12………………………………..……..2
EVALUATION
Solve the equations 3x+2y=7, 4x-2y=7 using method by elimination
ASSIGNMENT
(a) Solve the equation [sup](p-5q)[/sup]/[sub]2[/sub] = p-3, 5p-10q=16 simultaneously using any method of your choice
(b) Solve 2x+3y-1=3, 2x-2y=2 Using method by graph, method by elimination and method by substitution
READING ASSIGNMENT
Nelson Functional Mathematics for Junior Secondary school, book 3 Pg 87 – 91.
TOPIC: SIMILAR FIGURES AND ENLARGEMENT
CONTENT:
i. Concept of similar figures
ii. Examples of similar figures
iii. Enlargement and scale factor
SUB TOPIC: CONCEPT OF SIMILAR FIGURES
Two figures are similar, if they look alike and one is an enlargement or reduction of the other. Mathematically, if two shapes are similar, the ratio of their corresponding sides should be constant.
EXAMPLES OF SIMILAR FIGURES
(a) Similar photographs
Look at the photographs above. Although each of the two photographs are not of the same size, they look alike. We say that the pictures are similar to each other.
ENLARGEMENT AND SCALE FACTOR
The photograph in fig. a above is enlarged such that the sides are proportional. In this case, the ratio of the corresponding sides will be constant. Look at the example below.
Example 1
(a) Measure the length and breadth of the picture in fig. (a)
(b) Find the ratio length : breadth
(c) What do you notice?
Solution
(a) Length = 2cm, Breadth = 4cm (smaller picture)
Length = 2.4cm Breadth = 4.8cm (larger picture)
(b) Length :breadth = 4 : 2 = [sup]4[/sup]/[sub]2[/sub] = 2 (smaller picture)
Length : breadth = 4.8 : 2.4 = [sup]4.8[/sup]/[sub]2.4[/sub] = 2 (larger picture)
(c) The ratio of length to breadth for each picture is 2
Length : breadth is constant for both pictures in (a) this means that the first picture is an enlargement of the second picture. Hence when a shape is reduced or enlarged to give another shape such that the ratio of their corresponding sides are the same, we say, the two shapes are similar mathematically. This ratio is what we call the scale factor. The scale factor for the pictures in (a) is 2
Example 2
Consider the shapes below and indicate whether they are similar or not
Considering Fig. 1,
AB = 3.2cm
BC = 2.9cm
AC = 4.3cm
Similarly, in fig. 2,
PQ = 2.4cm
QR = 1.8cm
PR = 3.0cm
( AB)/PQ=[sup]3.2[/sup]/[sub]2.4[/sub] = 1.33
BC/QR=[sup]2.9[/sup]/[sub]1.8[/sub] = 1.61
AC/PR=[sup]4.2[/sup]/[sub]3.0[/sub] = 1.40
From the above calculations, it is clear that the ratios of the corresponding sides are not equal i.e AB/PQ≠BC/QR≠AC/PR. We therefore conclude that the two triangles are not similar.
QUESTIONS.
State whether the following statements are true or false
i. Two figures are similar, if one is a reduction of the other
ii. Two figures are not similar, if one is an enlargement of the other
iii. All isosceles triangles are similar
iv. All cuboids are similar
v. All pictures or images in the television are similar to the original bodies
vi All cubes are similar
EVALUATION
Consider the following shapes and indicate whether they are similar or not. Use measurement if you are not sure.
ASSIGNMENT
(Work book, Nelson Functional Mathematics for Junior secondary school, book 3). Page 44 and 45. Exercise A
WEEK 5
TOPIC: USE OF SCALE FACTOR IN CALCULATING LENGTHS, AREAS AND VOLUME OF SIMILAR FIGURES.
CONTENT: i. Scale Factor ( length ratio )
ii. Area of similar shapes
iii. Volume of similar shapes
SUB – TOPIC 1: SCALE FACTOR
When two shapes are similar, the ratio of their corresponding sides are the same. This ratio is called scale factor or length ratio.
Thus, the scale factor of two shapes is the ratio of two corresponding lengths.
Example
The scale factor of two similar triangles ABC and PQR shown below is 2.5. If AB = 12 cm and AC = 10 cm, find the length of (a) PQ (b) PR.
TOPIC: SOLVING SIMULTANEOUS EQUATIONS USING METHOD BY SUBSTITUTION AND BY ELIMINATION
CONTENT:
I. METHOD BY SUBSTITUTION
II. METHOD BY ELIMINATION
SUB TOPIC: METHOD BY SUBSTITUTION.
This is a method in which one variable is made the subject of the formula and substituted in the second equation. This will lead to a third equation with one variable. The equation is then solved for the value of the variable. This value can be substituted in any of the first two equations for the value of the second variable. See examples below.
Example 1.
Solve 2x+y=4……………..1
3x-y= -1[sup]1[/sup]/[sub]2[/sub] ……….2
using method by substitution
Solution
Example 2
Solve 3x-4y= - 6……………………………………..1
7x-2y=8………………………………………….2
Using method by substitution.
Solution
3x-4y=- 6 …………………………………………………………………eqn 1
7x-2y=8……………………………………………………………………..eqn 2
Now, put y=3 into eqn1
Thus, 3x-4(3)=- 6
3x-12=-6
Or 3x=12-6
3x=6
Thus, x=[sup]6[/sup]/[sub]3[/sub] = 2
Hence x=2,y=3 is the solution of the simultaneous equations
Check: 3(2)-4(3)=6-12=- 6……………………………………………eqn 1
7(2)-2(3)=14-6=8……………………………………………………….….eqn 2
EVALUATION
Using method by substitution, solve x-y=0, y-3x=1
METHOD BY ELIMINATION
Example 4
Solve 7x-2y=8……………………………………………………….1
3x-4y=-6…………………………………………………..…2
Solution:
Multiply eqn 1 by 4 and eqn 2 by 2
7x-2y=8………………………………eqn 1 x 4
3x-4y=-6……………………………eqn 2 x 2
4×7x-4×2y=8×4……………………….1
2×3x-2×4y=-6×2…………………….2
28x-8y=32………………………………………..1
6x-8y=-12………………………………..……..2
EVALUATION
Solve the equations 3x+2y=7, 4x-2y=7 using method by elimination
ASSIGNMENT
(a) Solve the equation [sup](p-5q)[/sup]/[sub]2[/sub] = p-3, 5p-10q=16 simultaneously using any method of your choice
(b) Solve 2x+3y-1=3, 2x-2y=2 Using method by graph, method by elimination and method by substitution
READING ASSIGNMENT
Nelson Functional Mathematics for Junior Secondary school, book 3 Pg 87 – 91.
TOPIC: SIMILAR FIGURES AND ENLARGEMENT
CONTENT:
i. Concept of similar figures
ii. Examples of similar figures
iii. Enlargement and scale factor
SUB TOPIC: CONCEPT OF SIMILAR FIGURES
Two figures are similar, if they look alike and one is an enlargement or reduction of the other. Mathematically, if two shapes are similar, the ratio of their corresponding sides should be constant.
EXAMPLES OF SIMILAR FIGURES
(a) Similar photographs
Look at the photographs above. Although each of the two photographs are not of the same size, they look alike. We say that the pictures are similar to each other.
ENLARGEMENT AND SCALE FACTOR
The photograph in fig. a above is enlarged such that the sides are proportional. In this case, the ratio of the corresponding sides will be constant. Look at the example below.
Example 1
(a) Measure the length and breadth of the picture in fig. (a)
(b) Find the ratio length : breadth
(c) What do you notice?
Solution
(a) Length = 2cm, Breadth = 4cm (smaller picture)
Length = 2.4cm Breadth = 4.8cm (larger picture)
(b) Length :breadth = 4 : 2 = [sup]4[/sup]/[sub]2[/sub] = 2 (smaller picture)
Length : breadth = 4.8 : 2.4 = [sup]4.8[/sup]/[sub]2.4[/sub] = 2 (larger picture)
(c) The ratio of length to breadth for each picture is 2
Length : breadth is constant for both pictures in (a) this means that the first picture is an enlargement of the second picture. Hence when a shape is reduced or enlarged to give another shape such that the ratio of their corresponding sides are the same, we say, the two shapes are similar mathematically. This ratio is what we call the scale factor. The scale factor for the pictures in (a) is 2
Example 2
Consider the shapes below and indicate whether they are similar or not
Considering Fig. 1,
AB = 3.2cm
BC = 2.9cm
AC = 4.3cm
Similarly, in fig. 2,
PQ = 2.4cm
QR = 1.8cm
PR = 3.0cm
( AB)/PQ=[sup]3.2[/sup]/[sub]2.4[/sub] = 1.33
BC/QR=[sup]2.9[/sup]/[sub]1.8[/sub] = 1.61
AC/PR=[sup]4.2[/sup]/[sub]3.0[/sub] = 1.40
From the above calculations, it is clear that the ratios of the corresponding sides are not equal i.e AB/PQ≠BC/QR≠AC/PR. We therefore conclude that the two triangles are not similar.
QUESTIONS.
State whether the following statements are true or false
i. Two figures are similar, if one is a reduction of the other
ii. Two figures are not similar, if one is an enlargement of the other
iii. All isosceles triangles are similar
iv. All cuboids are similar
v. All pictures or images in the television are similar to the original bodies
vi All cubes are similar
EVALUATION
Consider the following shapes and indicate whether they are similar or not. Use measurement if you are not sure.
ASSIGNMENT
(Work book, Nelson Functional Mathematics for Junior secondary school, book 3). Page 44 and 45. Exercise A
Solution
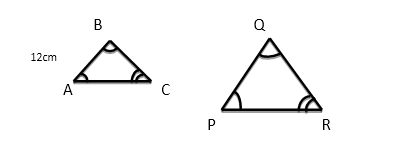
The scale factor of 2.5 means each corresponding side on triangle PQR is 2.5 times the corresponding length on triangle ABC.
PQ = AB x 2.5 = 12 x 2.5 = 30 cm
PR = AC x 2.5 = 10 x 2.5 = 25 cm
Determine the scale factor of the figures below.
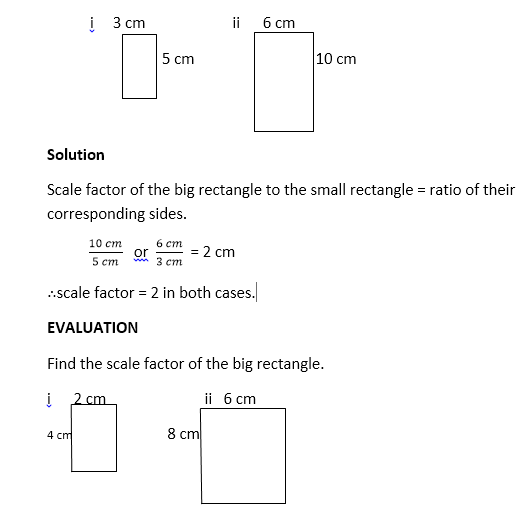
SUB–TOPIC 2 : AREA OF SIMILAR SHAPES
The ratio of the area of a figure to the area of the other similar figure is known as the area factor.
Examples
2. A fashion designer measured and instructed that a particular material 6 m by 4.5 m will make good birthday shirts for two brothers. If the elder brother is 1.5m, how tall is the younger brother?
Solution
3. Two similar cones have corresponding slant heights of 8 cm and 12 cm.
Find the ratio of their areas.
The area of the smaller cone is 102 cm2.
Calculate the area of the larger cone.
Solution
NOTE : The ratio of the areas of two similar shapes is the square of the scale factor of the two shapes.
EVALUATION
If the scale factor of a picture 15 cm long is 1 : 10, what is the length of the original object ?
Given that the ratio of the radii of two circles is [sup]3[/sup]/[sub]4[/sub] :
Find the ratio of their areas.
If the smaller circle has a radius of 12 cm, find the radius of the bigger circle.
Two similar triangle have corresponding sides of length 4 cm and 7 cm. find the ratio of their areas.
SUB-TOPIC 3: VOLUME OF SIMILAR SHAPES.
The ratio of the volumes of similar shapes could be compared to find the unknown parameters. This is possibly done using scale factor. The factor could be their edges, height or volume.
When the volumes of similar shapes are compared, the ratio of the volumes of the similar solids is the cube of the scale factor of the two solids.
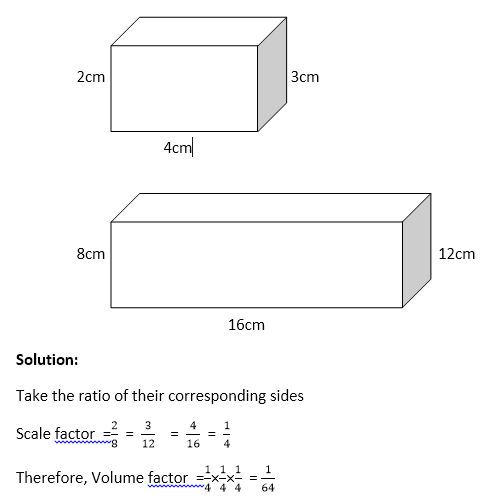
Examples
1. Using the dimensions of the similar shapes below, find their scale factor and the volume factor.
2. Two cylindrical pots similar in shape are respectively 5cm and 25cm high. If the smaller pot holds 1.5litres, find the capacity of the larger one.
a). Since mass = volume × density,
hence, mass is proportional to volume.
Thus, mass factor = [sup]1[/sup]/[sub]27[/sub]
Hence, ratio of their masses = 1 : 27
b). Mass of the larger block = 216g
Therefore, mass of the smaller block = [sup]216 ×1[/sup]/[sub]27[/sub] = 8g.
EVALUATION
The sides of two cuboids are in the ratio 3:5. What is the ratio of their volumes?
ASSIGNMENT:
Functional Mathematics BK 3, pg 162-164.
New General Mathematics BK 3, pg 179-180.
Functional Mathematics BK 3, pg 163, Ex. 10.3, No. 1-5.
New General Mathematics BK 3, pg 181, Ex. 18b, No. 1-5.
CONTENT: i. Scale Factor ( length ratio )
ii. Area of similar shapes
iii. Volume of similar shapes
SUB – TOPIC 1: SCALE FACTOR
When two shapes are similar, the ratio of their corresponding sides are the same. This ratio is called scale factor or length ratio.
Thus, the scale factor of two shapes is the ratio of two corresponding lengths.
Example
The scale factor of two similar triangles ABC and PQR shown below is 2.5. If AB = 12 cm and AC = 10 cm, find the length of (a) PQ (b) PR.
TOPIC: SOLVING SIMULTANEOUS EQUATIONS USING METHOD BY SUBSTITUTION AND BY ELIMINATION
CONTENT:
I. METHOD BY SUBSTITUTION
II. METHOD BY ELIMINATION
SUB TOPIC: METHOD BY SUBSTITUTION.
This is a method in which one variable is made the subject of the formula and substituted in the second equation. This will lead to a third equation with one variable. The equation is then solved for the value of the variable. This value can be substituted in any of the first two equations for the value of the second variable. See examples below.
Example 1.
Solve 2x+y=4……………..1
3x-y= -1[sup]1[/sup]/[sub]2[/sub] ……….2
using method by substitution
Solution
Example 2
Solve 3x-4y= - 6……………………………………..1
7x-2y=8………………………………………….2
Using method by substitution.
Solution
3x-4y=- 6 …………………………………………………………………eqn 1
7x-2y=8……………………………………………………………………..eqn 2
Now, put y=3 into eqn1
Thus, 3x-4(3)=- 6
3x-12=-6
Or 3x=12-6
3x=6
Thus, x=[sup]6[/sup]/[sub]3[/sub] = 2
Hence x=2,y=3 is the solution of the simultaneous equations
Check: 3(2)-4(3)=6-12=- 6……………………………………………eqn 1
7(2)-2(3)=14-6=8……………………………………………………….….eqn 2
EVALUATION
Using method by substitution, solve x-y=0, y-3x=1
METHOD BY ELIMINATION
Example 4
Solve 7x-2y=8……………………………………………………….1
3x-4y=-6…………………………………………………..…2
Solution:
Multiply eqn 1 by 4 and eqn 2 by 2
7x-2y=8………………………………eqn 1 x 4
3x-4y=-6……………………………eqn 2 x 2
4×7x-4×2y=8×4……………………….1
2×3x-2×4y=-6×2…………………….2
28x-8y=32………………………………………..1
6x-8y=-12………………………………..……..2
EVALUATION
Solve the equations 3x+2y=7, 4x-2y=7 using method by elimination
ASSIGNMENT
(a) Solve the equation [sup](p-5q)[/sup]/[sub]2[/sub] = p-3, 5p-10q=16 simultaneously using any method of your choice
(b) Solve 2x+3y-1=3, 2x-2y=2 Using method by graph, method by elimination and method by substitution
READING ASSIGNMENT
Nelson Functional Mathematics for Junior Secondary school, book 3 Pg 87 – 91.
TOPIC: SIMILAR FIGURES AND ENLARGEMENT
CONTENT:
i. Concept of similar figures
ii. Examples of similar figures
iii. Enlargement and scale factor
SUB TOPIC: CONCEPT OF SIMILAR FIGURES
Two figures are similar, if they look alike and one is an enlargement or reduction of the other. Mathematically, if two shapes are similar, the ratio of their corresponding sides should be constant.
EXAMPLES OF SIMILAR FIGURES
(a) Similar photographs
Look at the photographs above. Although each of the two photographs are not of the same size, they look alike. We say that the pictures are similar to each other.
ENLARGEMENT AND SCALE FACTOR
The photograph in fig. a above is enlarged such that the sides are proportional. In this case, the ratio of the corresponding sides will be constant. Look at the example below.
Example 1
(a) Measure the length and breadth of the picture in fig. (a)
(b) Find the ratio length : breadth
(c) What do you notice?
Solution
(a) Length = 2cm, Breadth = 4cm (smaller picture)
Length = 2.4cm Breadth = 4.8cm (larger picture)
(b) Length :breadth = 4 : 2 = [sup]4[/sup]/[sub]2[/sub] = 2 (smaller picture)
Length : breadth = 4.8 : 2.4 = [sup]4.8[/sup]/[sub]2.4[/sub] = 2 (larger picture)
(c) The ratio of length to breadth for each picture is 2
Length : breadth is constant for both pictures in (a) this means that the first picture is an enlargement of the second picture. Hence when a shape is reduced or enlarged to give another shape such that the ratio of their corresponding sides are the same, we say, the two shapes are similar mathematically. This ratio is what we call the scale factor. The scale factor for the pictures in (a) is 2
Example 2
Consider the shapes below and indicate whether they are similar or not
Considering Fig. 1,
AB = 3.2cm
BC = 2.9cm
AC = 4.3cm
Similarly, in fig. 2,
PQ = 2.4cm
QR = 1.8cm
PR = 3.0cm
( AB)/PQ=[sup]3.2[/sup]/[sub]2.4[/sub] = 1.33
BC/QR=[sup]2.9[/sup]/[sub]1.8[/sub] = 1.61
AC/PR=[sup]4.2[/sup]/[sub]3.0[/sub] = 1.40
From the above calculations, it is clear that the ratios of the corresponding sides are not equal i.e AB/PQ≠BC/QR≠AC/PR. We therefore conclude that the two triangles are not similar.
QUESTIONS.
State whether the following statements are true or false
i. Two figures are similar, if one is a reduction of the other
ii. Two figures are not similar, if one is an enlargement of the other
iii. All isosceles triangles are similar
iv. All cuboids are similar
v. All pictures or images in the television are similar to the original bodies
vi All cubes are similar
EVALUATION
Consider the following shapes and indicate whether they are similar or not. Use measurement if you are not sure.
ASSIGNMENT
(Work book, Nelson Functional Mathematics for Junior secondary school, book 3). Page 44 and 45. Exercise A
Solution
The scale factor of 2.5 means each corresponding side on triangle PQR is 2.5 times the corresponding length on triangle ABC.
PQ = AB x 2.5 = 12 x 2.5 = 30 cm
PR = AC x 2.5 = 10 x 2.5 = 25 cm
Determine the scale factor of the figures below.
SUB–TOPIC 2 : AREA OF SIMILAR SHAPES
The ratio of the area of a figure to the area of the other similar figure is known as the area factor.
Examples
2. A fashion designer measured and instructed that a particular material 6 m by 4.5 m will make good birthday shirts for two brothers. If the elder brother is 1.5m, how tall is the younger brother?
Solution
3. Two similar cones have corresponding slant heights of 8 cm and 12 cm.
Find the ratio of their areas.
The area of the smaller cone is 102 cm2.
Calculate the area of the larger cone.
Solution
NOTE : The ratio of the areas of two similar shapes is the square of the scale factor of the two shapes.
EVALUATION
If the scale factor of a picture 15 cm long is 1 : 10, what is the length of the original object ?
Given that the ratio of the radii of two circles is [sup]3[/sup]/[sub]4[/sub] :
Find the ratio of their areas.
If the smaller circle has a radius of 12 cm, find the radius of the bigger circle.
Two similar triangle have corresponding sides of length 4 cm and 7 cm. find the ratio of their areas.
SUB-TOPIC 3: VOLUME OF SIMILAR SHAPES.
The ratio of the volumes of similar shapes could be compared to find the unknown parameters. This is possibly done using scale factor. The factor could be their edges, height or volume.
When the volumes of similar shapes are compared, the ratio of the volumes of the similar solids is the cube of the scale factor of the two solids.
Examples
1. Using the dimensions of the similar shapes below, find their scale factor and the volume factor.
2. Two cylindrical pots similar in shape are respectively 5cm and 25cm high. If the smaller pot holds 1.5litres, find the capacity of the larger one.
a). Since mass = volume × density,
hence, mass is proportional to volume.
Thus, mass factor = [sup]1[/sup]/[sub]27[/sub]
Hence, ratio of their masses = 1 : 27
b). Mass of the larger block = 216g
Therefore, mass of the smaller block = [sup]216 ×1[/sup]/[sub]27[/sub] = 8g.
EVALUATION
The sides of two cuboids are in the ratio 3:5. What is the ratio of their volumes?
ASSIGNMENT:
Functional Mathematics BK 3, pg 162-164.
New General Mathematics BK 3, pg 179-180.
Functional Mathematics BK 3, pg 163, Ex. 10.3, No. 1-5.
New General Mathematics BK 3, pg 181, Ex. 18b, No. 1-5.
WEEK 7
TOPIC: TRIGONOMETRY
CONTENT: i. The trigonometric ratios
ii. Using Sine and Cosine Tables
iii Applications of sine and cosine
iv. The tangent of an acute angle
v. Applications of Trigonometric ratios to finding distances and lengths.
Sub Topic 1 : The Trigonometric ratios
A trigonometric ratio is a ratio of the lengths of two sides of a right – angled triangle. The three trigonometric ratios are sine ( sin), cosine ( cos ) and tangent ( tan ).
The figure below show triangle AHK in various positions
The sides of the triangles are as follows.
AH, the hypotenuse
KH, the side opposite to Ȃ
AK, the side adjacent to Ȃ
These are abbreviated to hyp, opp, adj, respectively, so that:
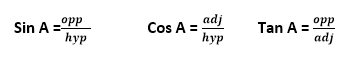
USE OF SINE
Sines and cosines of angles are used to find the lengths of unknown side in triangles. The table below gives the sines of some chosen angles.
Angle A... Sin A
30⁰ ...0.5000
35⁰ ...0.5736
40⁰ ...0.6428
45⁰ ...0.7071
50⁰ ...0.7660
55⁰ ...0.8192
60⁰ ...0.8660
The values in the table are given to 4 significant figures.
Example 1
Calculate the value of x in the figure below.
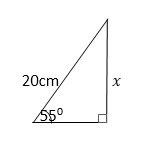
Solution
In the figure above, the hypotenuse is given and x is opposite the given angle. Thus ,
Sin 55⁰ = [sup]x[/sup]/[sub]20[/sub]
Thus, x= 20 x sin 55⁰
= 20 x 0.8192
= 16.384 cm
= 16 cm to 2 s.f.
USE OF COSINE
Angle A Cos A
30⁰ ...0.8660
35⁰ ...0.8192
40⁰ ...0.7660
45⁰ ...0.7071
50⁰ ...0.6428
55⁰ ...0.5736
60⁰ ...0.5000
Example 2 :
Calculate the value of y in the figure below.
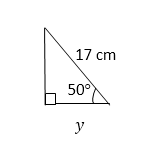
Solution
The hypotenuse is 17 cm and y is adjacent to the given angle. Thus use the cosine of the given angle.
Cos 50⁰ = [sup]y[/sup]/[sub]17[/sub]
Thus, y = 17 x cos 50⁰
= 17 x 0.642 8
= 10.93 cm
= 11 cm to 2 s.f
Example 3:
A village is 8 km on a bearing of 040⁰ from a point O. Calculate how far the village is north of O.
Solution
The figure below shows the position of the village,V in relation to O.
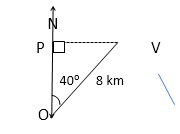
It is required to find the length of OP.
OP is adjacent to the known angle.
Use the cosine of 40⁰.
Cos 40⁰ = [sup]OP[/sup]/[sub]8[/sub]
Thus, OP = 8 x cos 40⁰ km
= 8 x 0.766 0 km
= 6.128 km
OP = 6.1 km to 2 s.f
The village is 6.1 km north of o.
EVALUATION:
Use the values in the tables above to answer the following questions. Give all answers correct to 2 s.f.
Find the values of x, y and z in each of the triangles bellow.
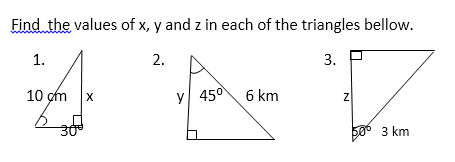
Sub Topic 2 : Using sine and cosine tables
Example 4:
Use tables to find the angles:
whose sine is = [sup]2[/sup]/[sub]7[/sub],
whose cosine is 0.4478,
whose sin is 0.649 2,
whose cosine is 0.568 2,
Solution
Let the angle be A, then sin A = [sup]2[/sup]/[sub]7[/sub].
Express [sup]2[/sup]/[sub]7[/sub] as a decimal fraction correct to 4 d.p.
2/7. = 0.285 7
Sin A = 0.285 7
Looking within the sine table entries,
0.2857 is opposite 16⁰ and under 0.6⁰.
Thus, A = 16.6⁰.
Let the angle be B, then cos B = 0.4478.
Looking within the cosine table entries,
0.447 8 is opposite 63⁰ and under 0.4.
Thus, B = 63.4⁰.
Let the angle be x, then sin x = 0.649 2.
Looking within the sin table entries, the nearest value to 0.649 2 is 0.648 1. 0.648 1 is opposite 40⁰ and under 0.4⁰.
The difference between 6 492 and 6 481 is 11. Look for 11 in the difference column along the row of 40⁰. 11 is under 8.
Thus, x = 40.40⁰ + 0.08⁰
X = 40.48⁰
Let the angle be y, then cos y = 0.568 2.
Looking within the cosine table entries, the nearest value to 0.568 2 is 0.567 8. 0.567 8 is opposite 55⁰ and under 0.4⁰. The difference between 5 682 and 5 678 is 4. Look for 4 in the difference column along the row of 55⁰.4 is under 3. As the angles increase, their cosines decrease, therefore subtract the difference.
Thus, y = 55.40⁰ - 0.03⁰
Y = 55.37⁰
EVALUATION:
Use tables to find the angles whose
Sines b. cosines are as follows.
0.5878 2. 0.798 6 3. 2/5 4. 0.564 8 5. 0.632 7
SUB TOPIC 3 :APPLICATIONS OF SINE AND COSINE
Example 5:
Calculate the length of the hypotenuse of the triangle below.
h 8 cm
43⁰
Solution
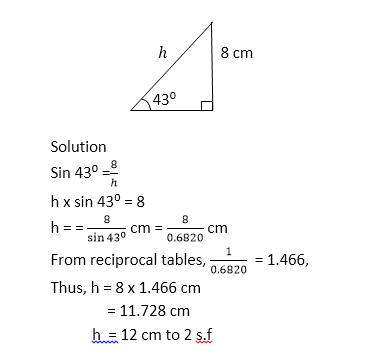
Example 6:
A car travels 120 m along a straight road which is inclined at 8⁰ to the horizontal. Calculate the vertical distance through which the car rises.
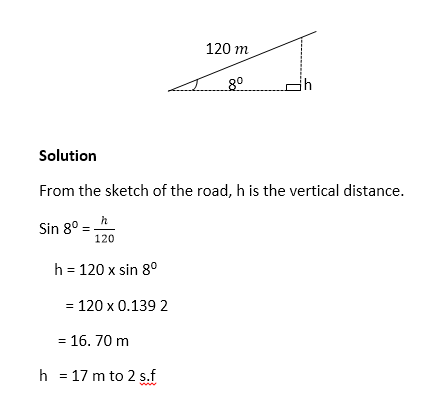
Solution
From the sketch of the road, h is the vertical distance.
Sin 8⁰ = h/120
h = 120 x sin 8⁰
= 120 x 0.139 2
= 16. 70 m
h = 17 m to 2 s.f
EVALUATION:
Calculate the lengths a, b, c, d, in the diagrams below. All lengths being in cm.
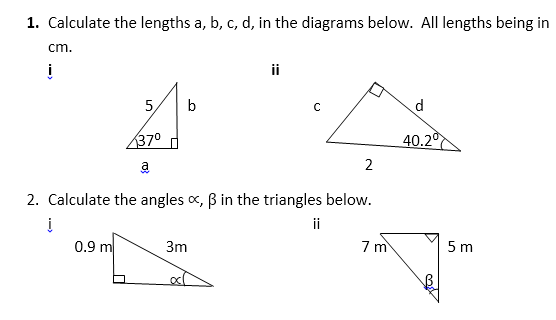
Sub Topic 4: Tangent of an acute angle
Tangents of some chosen angles
Angle A ...Tan A
25⁰ ...0.4663
30⁰ ...0.5774
35⁰ ...0.7002
40⁰ ...0.8391
45⁰ ...1.000
50⁰ ...1.192
55⁰ ...1.428
60⁰ ...1.732
65⁰ ...2.145
70⁰ ...2.747
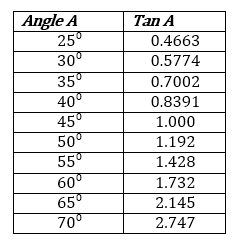
Example 7:
The angle of elevation of the top of a building is 25⁰ from a point 70 m away on a level ground. Calculate the height of the building.
Solution
HK represents the height of the building; AK is on level ground.
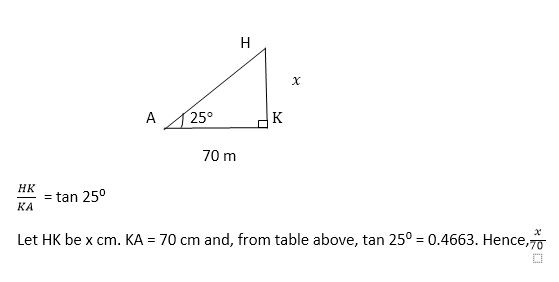
= 0.4663
X = 0.4663 x70
=4.663 x 7
= 32.641
∴The height of the building is 33 m to 2 s.f.
Example 8:
Use tables to find the tangents of angles
32⁰ b. 59.6⁰
Solution
Looking within the table entries, the number opposite 32⁰ and under 0.0⁰ is 0.6249.
Thus, tan 32⁰ = 0.6249.
The number opposite 59⁰ and under 0.6⁰ is 1.704. Thus, tan 59.6⁰ is 1.704. Thus, tan 59.6⁰ = 1.704.
Example 9:
Use tables to find the angles whose tangents are:
0.9556 b. [sup]7[/sup]/[sub]3[/sub]
Solution
Let the angle be A, then tan A = 0.9556. Looking within the table entries, 0.9556 is opposites 43⁰ and under 0.7⁰. Thus, A= 43.7⁰
Let the angle be B, then tan B = [sup]7[/sup]/[sub]3[/sub] = 2.333 to 4 S.f. Thus, B = 66.8⁰.
EVALUATION
Use table to find the value of x each triangles below.
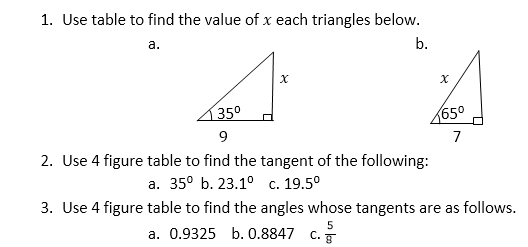
Use 4 figure table to find the tangent of the following:
35⁰ b. 23.1⁰ c. 19.5⁰
Use 4 figure table to find the angles whose tangents are as follows.
0.9325 b. 0.8847 c. [sup]5[/sup]/[sub]8[/sub]
SUB – TOPIC 5: APPLICATIONS OF TANGENTS
Tangent ratio can be used to solve real life problems such as angles of elevation and depressions and bearings.
Example 10:
A cone is 6 cm high and its vertical angle is 54⁰. Calculate the radius of its base.
Solution
The vertical angle is the angle between opposite slant heights VA and VB.
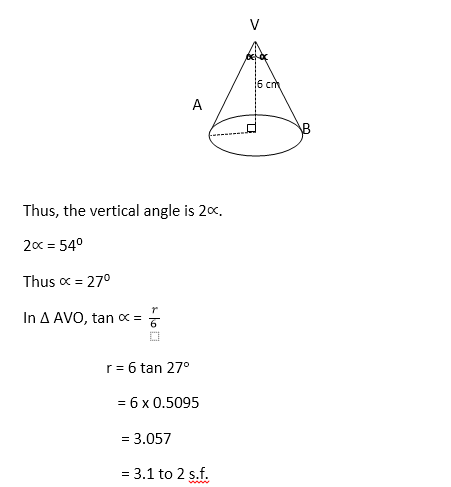
The radius of the base of the cone is 3.1 cm.
EVALUATION
A cone is 8 cm high and its vertical angle is 62°. Find the diameter of its base.
An isosceles triangle has a vertical angle of 116°, and its base is 8 cm long. Calculate its height.
Find the angle of elevation of the top of a flagpole 31.9 m high from a point 55 m away on level ground.
ASSIGNMENT
New General Mathematics for junior Secondary Schools 3 by M.F Macraeet. al. Exercise 8h pages 84 – 85,Questions 1 ( a – c), 2 ( a – d). Exercise 8d pages 79 & 80, Qs no 4 -6. Exercise 15b pages 145- 146, Qs no 4 – 7
READING ASSIGNMENT
New General Mathematics for junior Secondary Schools 2 by M.F Macraeet. al. Pages 196 – 198. Pages 223 – 227 .
CONTENT: i. The trigonometric ratios
ii. Using Sine and Cosine Tables
iii Applications of sine and cosine
iv. The tangent of an acute angle
v. Applications of Trigonometric ratios to finding distances and lengths.
Sub Topic 1 : The Trigonometric ratios
A trigonometric ratio is a ratio of the lengths of two sides of a right – angled triangle. The three trigonometric ratios are sine ( sin), cosine ( cos ) and tangent ( tan ).
The figure below show triangle AHK in various positions
The sides of the triangles are as follows.
AH, the hypotenuse
KH, the side opposite to Ȃ
AK, the side adjacent to Ȃ
These are abbreviated to hyp, opp, adj, respectively, so that:
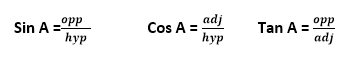
USE OF SINE
Sines and cosines of angles are used to find the lengths of unknown side in triangles. The table below gives the sines of some chosen angles.
Angle A... Sin A
30⁰ ...0.5000
35⁰ ...0.5736
40⁰ ...0.6428
45⁰ ...0.7071
50⁰ ...0.7660
55⁰ ...0.8192
60⁰ ...0.8660
The values in the table are given to 4 significant figures.
Example 1
Calculate the value of x in the figure below.
Solution
In the figure above, the hypotenuse is given and x is opposite the given angle. Thus ,
Sin 55⁰ = [sup]x[/sup]/[sub]20[/sub]
Thus, x= 20 x sin 55⁰
= 20 x 0.8192
= 16.384 cm
= 16 cm to 2 s.f.
USE OF COSINE
Angle A Cos A
30⁰ ...0.8660
35⁰ ...0.8192
40⁰ ...0.7660
45⁰ ...0.7071
50⁰ ...0.6428
55⁰ ...0.5736
60⁰ ...0.5000
Example 2 :
Calculate the value of y in the figure below.
Solution
The hypotenuse is 17 cm and y is adjacent to the given angle. Thus use the cosine of the given angle.
Cos 50⁰ = [sup]y[/sup]/[sub]17[/sub]
Thus, y = 17 x cos 50⁰
= 17 x 0.642 8
= 10.93 cm
= 11 cm to 2 s.f
Example 3:
A village is 8 km on a bearing of 040⁰ from a point O. Calculate how far the village is north of O.
Solution
The figure below shows the position of the village,V in relation to O.
It is required to find the length of OP.
OP is adjacent to the known angle.
Use the cosine of 40⁰.
Cos 40⁰ = [sup]OP[/sup]/[sub]8[/sub]
Thus, OP = 8 x cos 40⁰ km
= 8 x 0.766 0 km
= 6.128 km
OP = 6.1 km to 2 s.f
The village is 6.1 km north of o.
EVALUATION:
Use the values in the tables above to answer the following questions. Give all answers correct to 2 s.f.
Find the values of x, y and z in each of the triangles bellow.
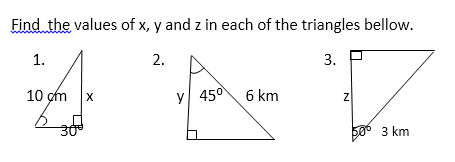
Sub Topic 2 : Using sine and cosine tables
Example 4:
Use tables to find the angles:
whose sine is = [sup]2[/sup]/[sub]7[/sub],
whose cosine is 0.4478,
whose sin is 0.649 2,
whose cosine is 0.568 2,
Solution
Let the angle be A, then sin A = [sup]2[/sup]/[sub]7[/sub].
Express [sup]2[/sup]/[sub]7[/sub] as a decimal fraction correct to 4 d.p.
2/7. = 0.285 7
Sin A = 0.285 7
Looking within the sine table entries,
0.2857 is opposite 16⁰ and under 0.6⁰.
Thus, A = 16.6⁰.
Let the angle be B, then cos B = 0.4478.
Looking within the cosine table entries,
0.447 8 is opposite 63⁰ and under 0.4.
Thus, B = 63.4⁰.
Let the angle be x, then sin x = 0.649 2.
Looking within the sin table entries, the nearest value to 0.649 2 is 0.648 1. 0.648 1 is opposite 40⁰ and under 0.4⁰.
The difference between 6 492 and 6 481 is 11. Look for 11 in the difference column along the row of 40⁰. 11 is under 8.
Thus, x = 40.40⁰ + 0.08⁰
X = 40.48⁰
Let the angle be y, then cos y = 0.568 2.
Looking within the cosine table entries, the nearest value to 0.568 2 is 0.567 8. 0.567 8 is opposite 55⁰ and under 0.4⁰. The difference between 5 682 and 5 678 is 4. Look for 4 in the difference column along the row of 55⁰.4 is under 3. As the angles increase, their cosines decrease, therefore subtract the difference.
Thus, y = 55.40⁰ - 0.03⁰
Y = 55.37⁰
EVALUATION:
Use tables to find the angles whose
Sines b. cosines are as follows.
0.5878 2. 0.798 6 3. 2/5 4. 0.564 8 5. 0.632 7
SUB TOPIC 3 :APPLICATIONS OF SINE AND COSINE
Example 5:
Calculate the length of the hypotenuse of the triangle below.
h 8 cm
43⁰
Solution
Example 6:
A car travels 120 m along a straight road which is inclined at 8⁰ to the horizontal. Calculate the vertical distance through which the car rises.
Solution
From the sketch of the road, h is the vertical distance.
Sin 8⁰ = h/120
h = 120 x sin 8⁰
= 120 x 0.139 2
= 16. 70 m
h = 17 m to 2 s.f
EVALUATION:
Calculate the lengths a, b, c, d, in the diagrams below. All lengths being in cm.
Sub Topic 4: Tangent of an acute angle
Tangents of some chosen angles
Angle A ...Tan A
25⁰ ...0.4663
30⁰ ...0.5774
35⁰ ...0.7002
40⁰ ...0.8391
45⁰ ...1.000
50⁰ ...1.192
55⁰ ...1.428
60⁰ ...1.732
65⁰ ...2.145
70⁰ ...2.747
Example 7:
The angle of elevation of the top of a building is 25⁰ from a point 70 m away on a level ground. Calculate the height of the building.
Solution
HK represents the height of the building; AK is on level ground.
= 0.4663
X = 0.4663 x70
=4.663 x 7
= 32.641
∴The height of the building is 33 m to 2 s.f.
Example 8:
Use tables to find the tangents of angles
32⁰ b. 59.6⁰
Solution
Looking within the table entries, the number opposite 32⁰ and under 0.0⁰ is 0.6249.
Thus, tan 32⁰ = 0.6249.
The number opposite 59⁰ and under 0.6⁰ is 1.704. Thus, tan 59.6⁰ is 1.704. Thus, tan 59.6⁰ = 1.704.
Example 9:
Use tables to find the angles whose tangents are:
0.9556 b. [sup]7[/sup]/[sub]3[/sub]
Solution
Let the angle be A, then tan A = 0.9556. Looking within the table entries, 0.9556 is opposites 43⁰ and under 0.7⁰. Thus, A= 43.7⁰
Let the angle be B, then tan B = [sup]7[/sup]/[sub]3[/sub] = 2.333 to 4 S.f. Thus, B = 66.8⁰.
EVALUATION
Use table to find the value of x each triangles below.
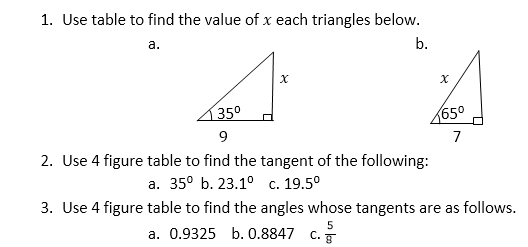
Use 4 figure table to find the tangent of the following:
35⁰ b. 23.1⁰ c. 19.5⁰
Use 4 figure table to find the angles whose tangents are as follows.
0.9325 b. 0.8847 c. [sup]5[/sup]/[sub]8[/sub]
SUB – TOPIC 5: APPLICATIONS OF TANGENTS
Tangent ratio can be used to solve real life problems such as angles of elevation and depressions and bearings.
Example 10:
A cone is 6 cm high and its vertical angle is 54⁰. Calculate the radius of its base.
Solution
The vertical angle is the angle between opposite slant heights VA and VB.
The radius of the base of the cone is 3.1 cm.
EVALUATION
A cone is 8 cm high and its vertical angle is 62°. Find the diameter of its base.
An isosceles triangle has a vertical angle of 116°, and its base is 8 cm long. Calculate its height.
Find the angle of elevation of the top of a flagpole 31.9 m high from a point 55 m away on level ground.
ASSIGNMENT
New General Mathematics for junior Secondary Schools 3 by M.F Macraeet. al. Exercise 8h pages 84 – 85,Questions 1 ( a – c), 2 ( a – d). Exercise 8d pages 79 & 80, Qs no 4 -6. Exercise 15b pages 145- 146, Qs no 4 – 7
READING ASSIGNMENT
New General Mathematics for junior Secondary Schools 2 by M.F Macraeet. al. Pages 196 – 198. Pages 223 – 227 .
WEEK 8
MAIN TOPIC: Angles of Elevation and Depression
SPECIFIC TOPIC: Angles of Elevation
PERFORMANCE OBJECTIVE: At the end of the lesson, the students should be able to:
Solves problems on angles of elevation.
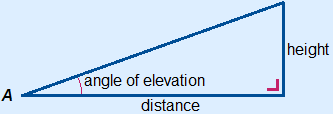
CONTENT: ANGLES OF ELEVATION
View diagram
When an observer looks at an object at a higher position, he/she has to raise or elevate his/her head.
Angle of elevation of an object at a higher position from an observer is the angle between the observer's line of sight and the horizontal.
Remarks: Angle of elevation is above the horizontal line.
Example 1: From a point 20m away from a tree, a man discovers that the angle of elevation of the tree is 400. If the man measured the angle of elevation from a point 2m above the ground, how high is the tree?
Solution
view diagram
https://skydrive.live.com/?sc=documents ... 2A33%21220
From the diagram above,
X = tan 400
20
X = 20 tan400
= 20(0.8391)
= 16.782m
The height of the tree = (x + 2)m
=16.782 + 2
= 18.782m
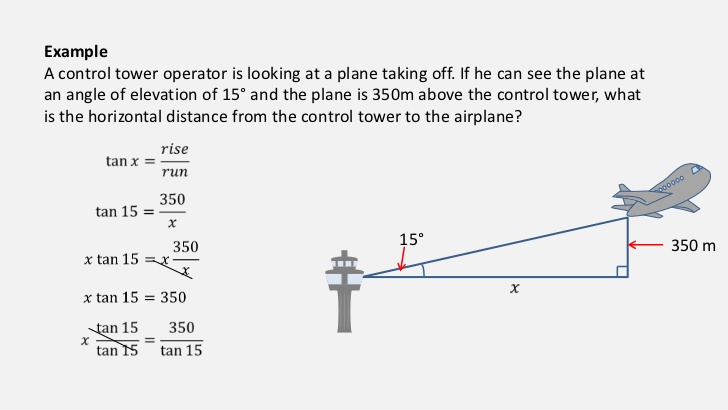
EVALUATION: solve the following problems.
A man 1.7m tall observes a bird on top of a tree at an angle of elevation of 400. If the distance between the man's head and the bird is 25m, what is the height of the tree?
ASSIGNMENT: A boy lying on the ground 30m away from the foot of a water tank tower observes that the angle of elevation of the top of the tank is 650. Calculate the height of the water tank.
MAIN TOPIC: Angles of Elevation and Depression
SPECIFIC TOPIC: Angles of Elevation
OBJECTIVE: At the end of the lesson, the students should be able to: Solve problems on elevation
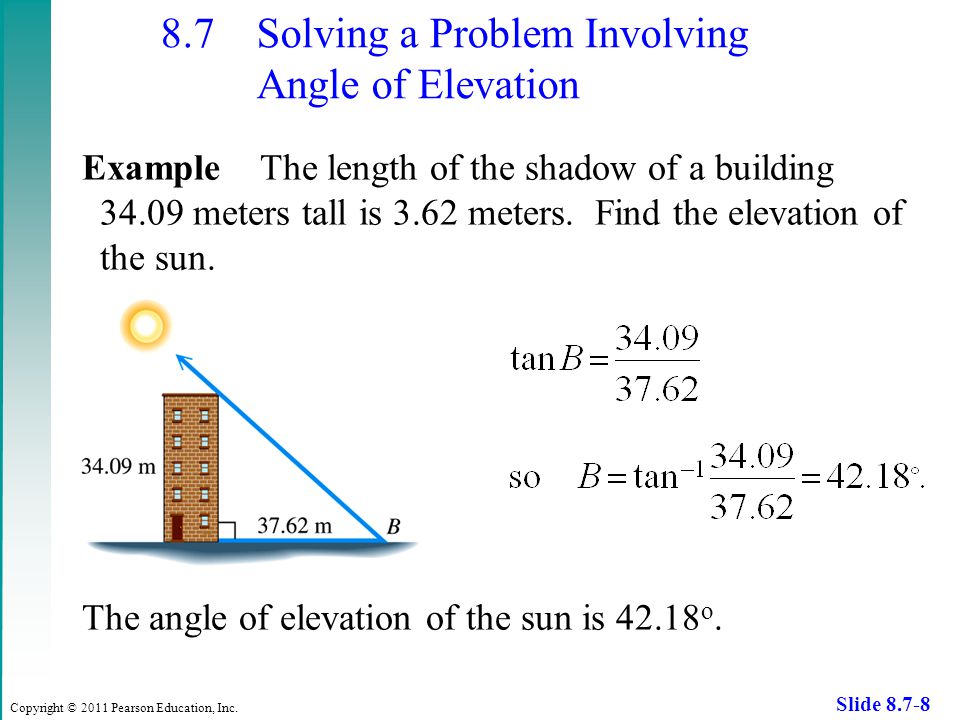
CONTENT: ANGLES OF ELEVATION
Example 1: The angle of elevation of the top of a vertical tower from a point A on the ground is 65˚. From a point 20m further away from the foot of the tower, the angle of elevation of the top of the tower is 50˚. Find the distance of A from the foot of the tower.
Solution
Let x be the required distance.
Let h be the height of the tower.
From ABC,
h = tan 65˚
x
h = x tan 65˚.............................(i)
From DBC,
h = tan50˚
x + 20
h = ( x+ 20) tan 50˚................(ii)
From (i) and (ii) above,
Xtan65˚ = (x + 20) tan50˚
X(tan 65˚ - tan 50˚) = 20 tan 50˚
X = 20tan50˚
Tan650 - tan50˚
X = 23.84
0.9528
= 25m(to the nearest whole number)
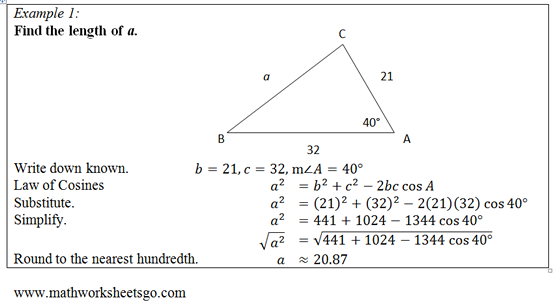
EVALUATION:
A flag-staff stands on the top of a vertical tower. A man standing 60m away from the tower observes that the angles of elevation of the top and bottom of the flag-staff are 64˚ and 62˚ respectively. Find the length of the flag-staff.
ASSIGNMENT:
The angle of elevation of the sun is 27˚. A man is 1.8 tall. How long is his shadow?
further studies
http://www.syvum.com/cgi/online/serve.c ... stion_hide
practice test
http://www.algebralab.org/Word/Word.asp ... ession.xml
MAIN TOPIC: Angles of Elevation and Depression
SPECIFIC TOPIC: Angles of Depression
OBJECTIVE: At the end of the lesson, the students should be able to:
Solve problems on angles of depression.
CONTENT: ANGLES OF DEPRESSION
When an observer looks at an object located in a lower position, he/she has to lower or depress his/her head.
Angle of depression of an object at a lower position from an observer is the angle between the observer's line of sight and the horizontal.
Remark: Angle of depression is below the horizontal line.
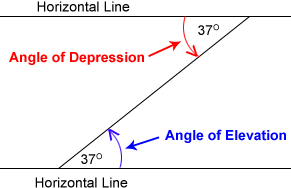
Example 1 : The angle of depression of a boat from the top of a cliff 10m high is 35˚. How far is the boat from the foot of the cliff?
Solution:
X = tan55˚
10
X =10tan55˚
= 14.28m.
The required distance is 14.28m.
EVALUATION:
From the top of a cliff 20m high, a boat can be sighted at sea 75m from the foot of the cliff. Calculate the angle of depression of the boat from the top of the cliff.
ASSIGNMENT:
The angle of depression of a boat from the top of a cliff 15m high is 30˚. How far is the boat from the foot of the cliff?
further studies
http://www.mathwords.com/a/angle_depression.htm
http://www.northstarmath.com/sitemap/An ... ssion.html
practice test
http://www.algebralab.org/practice/prac ... ssion1.xml
further studies
http://www.mathsteacher.com.au/year10/c ... levdep.htm
http://www.mathwarehouse.com/geometry/a ... /index.php
http://www.onlinemathlearning.com/angle ... ation.html
watch video
[youtube]http://www.youtube.com/watch?v=oLsZB1VzxQo[/youtube]
SPECIFIC TOPIC: Angles of Elevation
PERFORMANCE OBJECTIVE: At the end of the lesson, the students should be able to:
Solves problems on angles of elevation.
CONTENT: ANGLES OF ELEVATION
View diagram
When an observer looks at an object at a higher position, he/she has to raise or elevate his/her head.
Angle of elevation of an object at a higher position from an observer is the angle between the observer's line of sight and the horizontal.
Remarks: Angle of elevation is above the horizontal line.
Example 1: From a point 20m away from a tree, a man discovers that the angle of elevation of the tree is 400. If the man measured the angle of elevation from a point 2m above the ground, how high is the tree?
Solution
view diagram
https://skydrive.live.com/?sc=documents ... 2A33%21220
From the diagram above,
X = tan 400
20
X = 20 tan400
= 20(0.8391)
= 16.782m
The height of the tree = (x + 2)m
=16.782 + 2
= 18.782m
EVALUATION: solve the following problems.
A man 1.7m tall observes a bird on top of a tree at an angle of elevation of 400. If the distance between the man's head and the bird is 25m, what is the height of the tree?
ASSIGNMENT: A boy lying on the ground 30m away from the foot of a water tank tower observes that the angle of elevation of the top of the tank is 650. Calculate the height of the water tank.
MAIN TOPIC: Angles of Elevation and Depression
SPECIFIC TOPIC: Angles of Elevation
OBJECTIVE: At the end of the lesson, the students should be able to: Solve problems on elevation
CONTENT: ANGLES OF ELEVATION
Example 1: The angle of elevation of the top of a vertical tower from a point A on the ground is 65˚. From a point 20m further away from the foot of the tower, the angle of elevation of the top of the tower is 50˚. Find the distance of A from the foot of the tower.
Solution
Let x be the required distance.
Let h be the height of the tower.
From ABC,
h = tan 65˚
x
h = x tan 65˚.............................(i)
From DBC,
h = tan50˚
x + 20
h = ( x+ 20) tan 50˚................(ii)
From (i) and (ii) above,
Xtan65˚ = (x + 20) tan50˚
X(tan 65˚ - tan 50˚) = 20 tan 50˚
X = 20tan50˚
Tan650 - tan50˚
X = 23.84
0.9528
= 25m(to the nearest whole number)
EVALUATION:
A flag-staff stands on the top of a vertical tower. A man standing 60m away from the tower observes that the angles of elevation of the top and bottom of the flag-staff are 64˚ and 62˚ respectively. Find the length of the flag-staff.
ASSIGNMENT:
The angle of elevation of the sun is 27˚. A man is 1.8 tall. How long is his shadow?
further studies
http://www.syvum.com/cgi/online/serve.c ... stion_hide
practice test
http://www.algebralab.org/Word/Word.asp ... ession.xml
MAIN TOPIC: Angles of Elevation and Depression
SPECIFIC TOPIC: Angles of Depression
OBJECTIVE: At the end of the lesson, the students should be able to:
Solve problems on angles of depression.
CONTENT: ANGLES OF DEPRESSION
When an observer looks at an object located in a lower position, he/she has to lower or depress his/her head.
Angle of depression of an object at a lower position from an observer is the angle between the observer's line of sight and the horizontal.
Remark: Angle of depression is below the horizontal line.
Example 1 : The angle of depression of a boat from the top of a cliff 10m high is 35˚. How far is the boat from the foot of the cliff?
Solution:
X = tan55˚
10
X =10tan55˚
= 14.28m.
The required distance is 14.28m.
EVALUATION:
From the top of a cliff 20m high, a boat can be sighted at sea 75m from the foot of the cliff. Calculate the angle of depression of the boat from the top of the cliff.
ASSIGNMENT:
The angle of depression of a boat from the top of a cliff 15m high is 30˚. How far is the boat from the foot of the cliff?
further studies
http://www.mathwords.com/a/angle_depression.htm
http://www.northstarmath.com/sitemap/An ... ssion.html
practice test
http://www.algebralab.org/practice/prac ... ssion1.xml
further studies
http://www.mathsteacher.com.au/year10/c ... levdep.htm
http://www.mathwarehouse.com/geometry/a ... /index.php
http://www.onlinemathlearning.com/angle ... ation.html
watch video
[youtube]http://www.youtube.com/watch?v=oLsZB1VzxQo[/youtube]
WEEK 9
TOPIC: AREA OF PLANE FIGURES
CONTENT:
i. Area of basic shapes: Revision ( triangles, rectangles, trapeziums, parallelogram and circles )
ii. Using trigonometry in area problems
iii. Area of circles and sectors
iv. Land measure
SUB – TOPIC 1. AREA OF BASIC SHAPES
The formulae for areas of some basic shapes are given in below. These were previously found in book 1, Chapter 14.
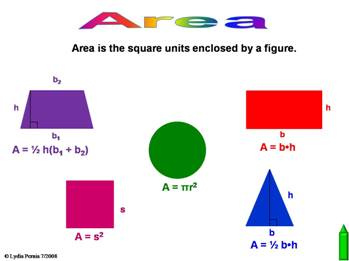
Area of rectangle = length x breadth = ( l x b )
Area of trapezium = [sup]1[/sup]/[sub]2[/sub] of ( sum of parallel sides ) x height = [sup]1[/sup]/[sub]2[/sub] ( a + b )h
Area of parallelogram = base x height = b x h
Area of circle = πr[sup]2[/sup]
Area of triangle = [sup]1[/sup]/[sub]2[/sub] x product of sides containing the right angle.
Examples:
Find the area of a triangle with base 15 cm and height 9 cm.
Solution
Area of triangle = [sup]1[/sup]/[sub]2[/sub] @)base x height
= [sup]1[/sup]/[sub]2[/sub] x 15 x 9
= 67.5 cm[sup]2[/sup]
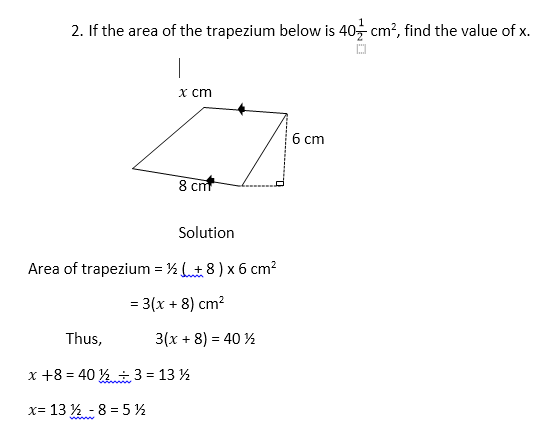
EVALUATION
1. The seconds hand of a watch is 14 mm long. What area does it sweep through in 30 seconds?
2. A goat is tied by a rope 2 ½ m long to a peg in some grass. The goat eats 1 m2 of grass in 28 min. How long will it take to eat all that it can reach?
3. A triangle has area of 35 cm2 and a base of 10 cm. Find the height of the triangle.
SUB – TOPIC 2: USING TRIGONOMETRY IN AREA PROBLEMS
Examples:
Find the area of ∆ABC to the nearest cm2 if BA = 6 cm, BC = 7 cm and B ̂ = 34°.
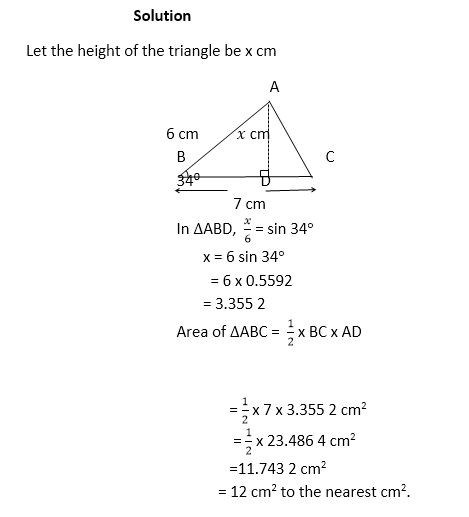
For a parallelogram with non – parallel sides a, b containing an angle θ.
Area of parallelogram = ab sin θ
EVALUATION
1. The area of a parallelogram is 240 cm2. The angle between the two adjacent sides of the parallelogram is 145°. If the length of one of the adjacent side is 16 cm, find the length of the other side correct to the nearest cm.
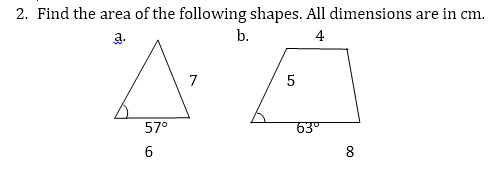
SUB – TOPIC 3: AREA OF CIRCLES AND SECTORS
A sector is part of a circle bounded by an arc and two radii.
In the diagram bellow, O is the centre, AO and AB divide the inside of the circle into two parts called sectors. The smaller is called the minor sector (shaded ), and the larger is called the major sector ( unshaded )
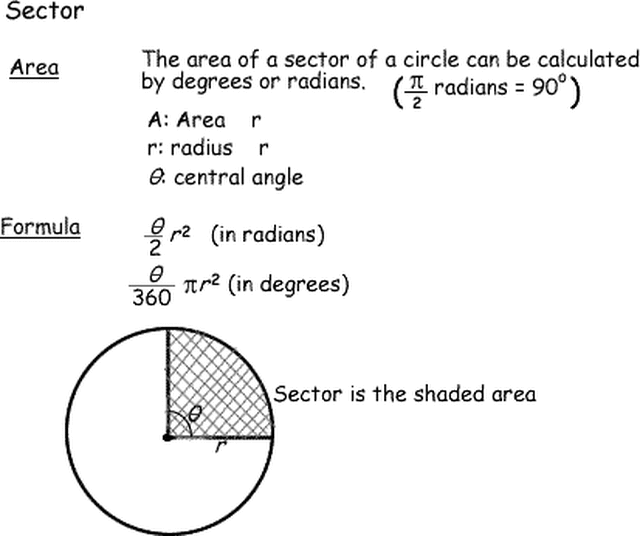
Examples:
1. What is the area of a flat washer 4.8 cm in outside diameter, the hole being of diameter 2.2 cm?
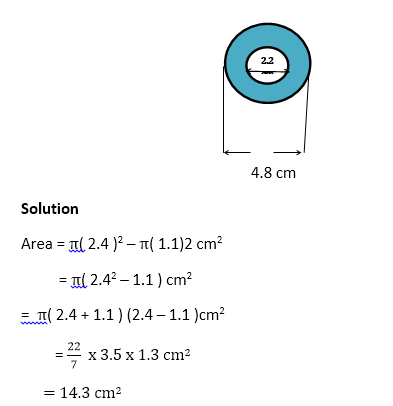
2. Find the area of a sector of radius 7 cm , the angle at the centre of the circle being 108°.
Solution
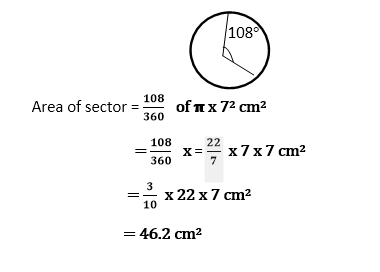
EVALUATION
The area of a sector of a circle is 44 cm2. What is the radius of the circle if the angle subtended at the centre is 140°?
A sector of a circle of radius 8 cm has an angle of 120° at the centre.
Find its perimeter
Find its area ( take π = 3.142 )
Hint: perimeter = length of minor arc + radii.
Length of arc = [sup]θ[/sup]/[sub]360[/sub] x 2πr
Find the area between two circles with the same centre and of radius 5 cm and 9 cm respectively. Take π = [sup]22[/sup]/[sub]7[/sub]
CONTENT:
i. Area of basic shapes: Revision ( triangles, rectangles, trapeziums, parallelogram and circles )
ii. Using trigonometry in area problems
iii. Area of circles and sectors
iv. Land measure
SUB – TOPIC 1. AREA OF BASIC SHAPES
The formulae for areas of some basic shapes are given in below. These were previously found in book 1, Chapter 14.
Area of rectangle = length x breadth = ( l x b )
Area of trapezium = [sup]1[/sup]/[sub]2[/sub] of ( sum of parallel sides ) x height = [sup]1[/sup]/[sub]2[/sub] ( a + b )h
Area of parallelogram = base x height = b x h
Area of circle = πr[sup]2[/sup]
Area of triangle = [sup]1[/sup]/[sub]2[/sub] x product of sides containing the right angle.
Examples:
Find the area of a triangle with base 15 cm and height 9 cm.
Solution
Area of triangle = [sup]1[/sup]/[sub]2[/sub] @)base x height
= [sup]1[/sup]/[sub]2[/sub] x 15 x 9
= 67.5 cm[sup]2[/sup]
EVALUATION
1. The seconds hand of a watch is 14 mm long. What area does it sweep through in 30 seconds?
2. A goat is tied by a rope 2 ½ m long to a peg in some grass. The goat eats 1 m2 of grass in 28 min. How long will it take to eat all that it can reach?
3. A triangle has area of 35 cm2 and a base of 10 cm. Find the height of the triangle.
SUB – TOPIC 2: USING TRIGONOMETRY IN AREA PROBLEMS
Examples:
Find the area of ∆ABC to the nearest cm2 if BA = 6 cm, BC = 7 cm and B ̂ = 34°.
For a parallelogram with non – parallel sides a, b containing an angle θ.
Area of parallelogram = ab sin θ
EVALUATION
1. The area of a parallelogram is 240 cm2. The angle between the two adjacent sides of the parallelogram is 145°. If the length of one of the adjacent side is 16 cm, find the length of the other side correct to the nearest cm.
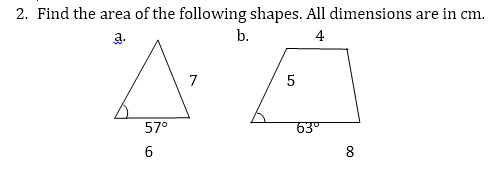
SUB – TOPIC 3: AREA OF CIRCLES AND SECTORS
A sector is part of a circle bounded by an arc and two radii.
In the diagram bellow, O is the centre, AO and AB divide the inside of the circle into two parts called sectors. The smaller is called the minor sector (shaded ), and the larger is called the major sector ( unshaded )
Examples:
1. What is the area of a flat washer 4.8 cm in outside diameter, the hole being of diameter 2.2 cm?
2. Find the area of a sector of radius 7 cm , the angle at the centre of the circle being 108°.
Solution
EVALUATION
The area of a sector of a circle is 44 cm2. What is the radius of the circle if the angle subtended at the centre is 140°?
A sector of a circle of radius 8 cm has an angle of 120° at the centre.
Find its perimeter
Find its area ( take π = 3.142 )
Hint: perimeter = length of minor arc + radii.
Length of arc = [sup]θ[/sup]/[sub]360[/sub] x 2πr
Find the area between two circles with the same centre and of radius 5 cm and 9 cm respectively. Take π = [sup]22[/sup]/[sub]7[/sub]
REVISION
PRACTICE TEST 1
http://quiz.econ.usyd.edu.au/mathquiz/s ... /index.php
http://www.suffolkmaths.co.uk/pages/1Al ... ources.htm
http://www.onlinemathlearning.com/algebra-help.html
http://www.softschools.com/quizzes/math/
http://www.glencoe.com/sec/math/algebra ... ex.php4/na
http://mymcas.com/html_pages/quizzes.htm
http://www.ischool.zm/1417/grade_11/p29 ... &subhide=1
http://www.classzone.com/books/geometry ... tional.cfm
http://quiz.econ.usyd.edu.au/mathquiz/s ... /index.php
http://www.suffolkmaths.co.uk/pages/1Al ... ources.htm
http://www.onlinemathlearning.com/algebra-help.html
http://www.softschools.com/quizzes/math/
http://www.glencoe.com/sec/math/algebra ... ex.php4/na
http://mymcas.com/html_pages/quizzes.htm
http://www.ischool.zm/1417/grade_11/p29 ... &subhide=1
http://www.classzone.com/books/geometry ... tional.cfm
