3RD TERM
3RD TERM
SCHEME OF WORK
WEEKS TOPICS
1. Revision of last term's work
2. Geometry
- Plane shapes (types and perimeter)
3. Geometry
- Area of regular and irregular shapes.
4. Three dimensional figures
- Properties of cube, cuboids, pyramid, cone, cylinders, spheres.
5. Properties of solid shapes.
- Volume of cube and cuboids.
6. Identification and properties of angle a
(Vertically opposite, adjacent, alternate, corresponding angles)
7. The sum of angles on a straight line and in a triangle.
8. Construction of Parallel lines, perpendicular lines, measurement of angles.
9. Statistics
- purposes and usefulness of statistics for analysis, data collection.
10. Data presentation - Averages, mean, median, mode of a given set of data.
11. Revision
WEEKS TOPICS
1. Revision of last term's work
2. Geometry
- Plane shapes (types and perimeter)
3. Geometry
- Area of regular and irregular shapes.
4. Three dimensional figures
- Properties of cube, cuboids, pyramid, cone, cylinders, spheres.
5. Properties of solid shapes.
- Volume of cube and cuboids.
6. Identification and properties of angle a
(Vertically opposite, adjacent, alternate, corresponding angles)
7. The sum of angles on a straight line and in a triangle.
8. Construction of Parallel lines, perpendicular lines, measurement of angles.
9. Statistics
- purposes and usefulness of statistics for analysis, data collection.
10. Data presentation - Averages, mean, median, mode of a given set of data.
11. Revision
WEEK 1
Topic : Geometry- plane shapes
Contents:
Perimeter of a regular polygon
Perimeter of a square
Perimeter of a rectangle
Perimeter of a triangle
Perimeter of a trapezium
Perimeter of a parallelogram
Perimeter of a circle
MEASURING PERIMETERS
Perimeter is the outside boundary or edge of a plane shape. For example, the boundary fence of your school compound is its perimeter. We also use the word perimeter to mean the length of the boundary. For example , if you take 200 paces to walk your school boundary, you could say its perimeter is 200 paces.
PERIMETER OF A REGULAR POLYGON
The simplest way to find a perimeter of any regular shape is to measure it directly with a ruler. Or tape measure.
Examples;
Find, in cm the perimeter of the regular hexagon ABCDEF in Fig. 1.0.
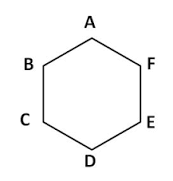
Length of side AB = 1.6 cm.
There are 6 equal sides, so
Perimeter = 6 × 1.6cm
=9.6 cm
If a shape has a curved side, use a piece of thread to get the shape of the curve. Make the thread to get the shape of the curve. Make the thread straight and measure its length against a ruler.
2. Measure the Perimeter of the shape in the fig below.
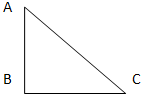
Straight edges: AB = 14 mm =1.4 cm
BC =14 mm =1.4 cm
Curved edge: CA =22mm approximately
=2.2cm
Perimeter (total = 50 mm approximately
= 5.0 cm
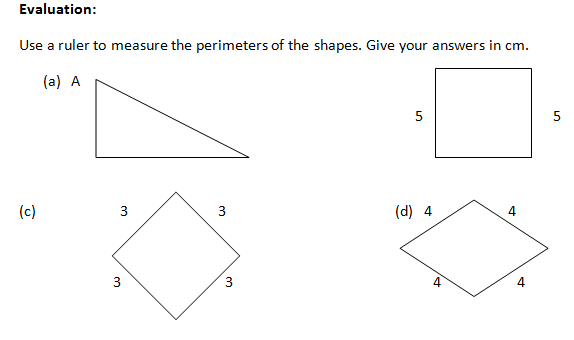
Evaluation:
Draw and Use a ruler to measure the perimeters of the shape illustrated above. Give your answer in cm.
(a)
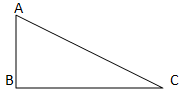
Straight edges : AB = 14 mm = 1.4 cm
BC = 14mm = 1.4 cm
Curved edge : CA = 22 mm approximately
= 2.2 cm
Perimeter (total ) = 50 mm approximately
= 5.0 cm
PERIMETER OF A SQUARE
A square is a regular four- sided shape. If the length of one side of a square is l, then,
Perimeter of square = l × 4
= 4l
As perimeter of square =4l,
Length of side of square = perimeter of square
4
Example ;
(1) Calculate the perimeter of a square of side 12.3cm.
Solution
Perimeter = 12.3cm × 4
Perimeter = 49.2 cm
(2) A square assembly area has a perimeter of 56m. Find the length of the assembly area.
Solution
Length = 56
4
= 14m.
Note: The formulae for perimeters of rectangles and squares can be useful. However, if you find it difficult to remember formulae, always sketch the given shape and work from that.

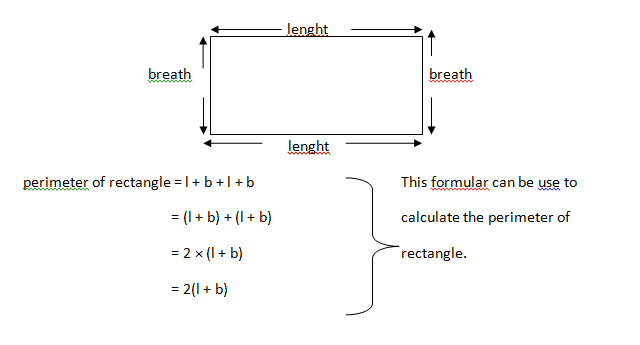
PERIMETER OF RECTANGLES
The longer side of a rectangle is called length , and the shorter side is calledbreadth . We use the letter l and b to stand for the length and the breath.
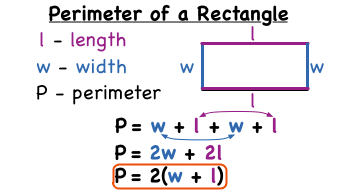
perimeter of rectangle = l + b + l + b This formular can be use to
= (l + b) + (l + b) calculate the perimeter of
= 2 × (l + b) rectangle.
= 2(l + b)
Example
Calculate the perimeter of a football field which measures 80m by 50m.
Solution
Perimeter of field = 2(l+ b)
= 2 × (80 + 50) m
= 2 × 130m
= 260m.
(3) A rectangular piece of land measures 57 m by 42m. What is the perimeter of the perimeter of the land ?
Perimeter of land = 2(l+ b)
= 2(57+ 45)m
= 2× 99m
= 198m.
AREA OF A TRIANGLES
Any diagonal of a rectangle divided it into two equal right- angled triangles.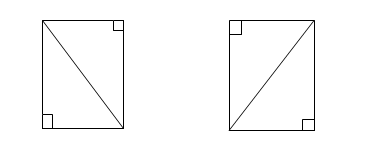
Thus :
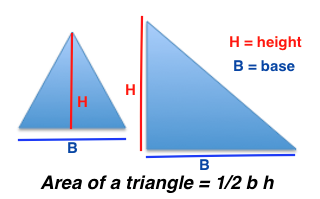
Area of a right – angled triangle
= ½ × product of sides containing the right angle.
Area of triangle = ½ × base × height.
Example:
Calculate the area of the triangle shown below;
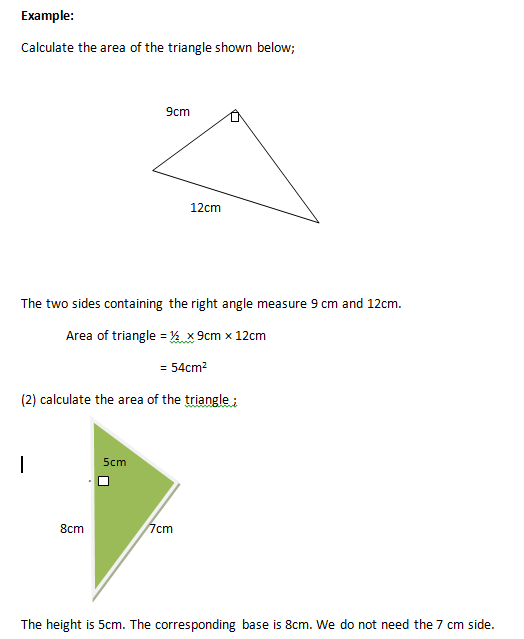
The two sides containing the right angle measure 9 cm and 12cm.
Area of triangle = ½ × 9cm × 12cm
= 54cm2
(2) calculate the area of the triangle with height 5cm, base 8cm and hypotenuse 7cm.
The height is 5cm. The corresponding base is 8cm. We do not need the 7 cm side.
Solution:
Area of triangle = ½ ×base × height
= ½ × 8cm × 5cm
= 20cm2
Evaluation:
New general mathematics for junior secondary schools 1 UBE Edition.
Exercise 14d 1(a) –(d) page 120.
AREA OF A TRAPEZIUMS:

ABCD is a trapezium in which AB is parallel to DC. The diagonal AD divides the trapezium into two triangles. The height, h, is the same for both triangles.
area of trapezium ABCD
= area of ABD + area of BDC
½ AB × h + ½ DC × h
= ½ (AB + DC)h
Example:
Calculate the area of the trapezium ABCD in figure below;
The diagonal AC divides the trapezium into two triangles. The height of each triangle is 8 cm.
Area of ACB = ½ × 13cm × 8cm =52cm2
Area of ACD = ½ × 6cm × 8cm = 24cm2
Area of trapezium = 52cm2 + 24cm2 =76cm2
Evaluation:
New general mathematics for junior secondary school 1 UBE Edition,
Exercise : 14d no’s: 2(a) – (d).
Area of parallelograms
A parallelogram can have two bases and two corresponding heights as show below;
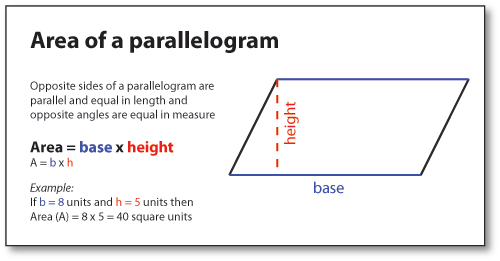
Area (A) = base (1) × height (1)
Also area (A) =base(2) × height (2)
Therefore base (1) × height (2) × height (2)
Example:
Calculate the area of the paralellograms below. All dimensions are in centimeters.
base = 5
height = 7
(a) Area of parallelogram = base × height
= 7cm × 5 cm
= 35cm
base = 5
height = 3
(b) Area of parallelogram = base × height
= 5cm × 3cm
= 15cm.
Evaluation:
1. Calculate the area of a parallelogram if its base is 9.2cm and its height is 6cm
2. the area of a parallelogram is 99cm2 its base is 11cm. calculate the corresponding height of the parallogram
3. calculate the base of a parallelogram whose area and height is 27cm and 9cm respectively.
Area of a circles
Area of a circle = ∏r2
∏ = 22/7
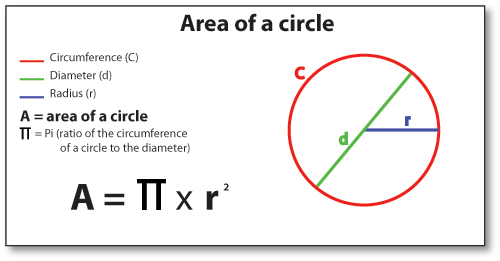
Diameter= 2r. where r = radius
Example:
(1) Find the area of a circle whose radius is 3½m. Taken∏to be 22/7
Solution:
area of a circle = ∏r2
= 22/7 × (3½)2= 22/7 × 7/2 × 7/2m2
= 11 × 7
2
= 381/2 m2

Evaluation:
New general mathematics for junior secondary schools 1 UBE Edition . Exercise 14e 1(a)- (f) page 122. take ∏= 22/7
Reading assignment:
New general mathematics for junior secondary schools 1 UBE Edition. Page 116- 123.
assignment:
New general mathematics for junior secondary schools 1 UBE Edition. Page116 -123. Exercise 14e 3(a) –(f), Exercise 14d 1 (a) – (e).
Contents:
Perimeter of a regular polygon
Perimeter of a square
Perimeter of a rectangle
Perimeter of a triangle
Perimeter of a trapezium
Perimeter of a parallelogram
Perimeter of a circle
MEASURING PERIMETERS
Perimeter is the outside boundary or edge of a plane shape. For example, the boundary fence of your school compound is its perimeter. We also use the word perimeter to mean the length of the boundary. For example , if you take 200 paces to walk your school boundary, you could say its perimeter is 200 paces.
PERIMETER OF A REGULAR POLYGON
The simplest way to find a perimeter of any regular shape is to measure it directly with a ruler. Or tape measure.
Examples;
Find, in cm the perimeter of the regular hexagon ABCDEF in Fig. 1.0.

Length of side AB = 1.6 cm.
There are 6 equal sides, so
Perimeter = 6 × 1.6cm
=9.6 cm
If a shape has a curved side, use a piece of thread to get the shape of the curve. Make the thread to get the shape of the curve. Make the thread straight and measure its length against a ruler.
2. Measure the Perimeter of the shape in the fig below.

Straight edges: AB = 14 mm =1.4 cm
BC =14 mm =1.4 cm
Curved edge: CA =22mm approximately
=2.2cm
Perimeter (total = 50 mm approximately
= 5.0 cm
Evaluation:
Draw and Use a ruler to measure the perimeters of the shape illustrated above. Give your answer in cm.
(a)

Straight edges : AB = 14 mm = 1.4 cm
BC = 14mm = 1.4 cm
Curved edge : CA = 22 mm approximately
= 2.2 cm
Perimeter (total ) = 50 mm approximately
= 5.0 cm

PERIMETER OF A SQUARE
A square is a regular four- sided shape. If the length of one side of a square is l, then,
Perimeter of square = l × 4
= 4l
As perimeter of square =4l,
Length of side of square = perimeter of square
4
Example ;
(1) Calculate the perimeter of a square of side 12.3cm.
Solution
Perimeter = 12.3cm × 4
Perimeter = 49.2 cm
(2) A square assembly area has a perimeter of 56m. Find the length of the assembly area.
Solution
Length = 56
4
= 14m.
Note: The formulae for perimeters of rectangles and squares can be useful. However, if you find it difficult to remember formulae, always sketch the given shape and work from that.

PERIMETER OF RECTANGLES
The longer side of a rectangle is called length , and the shorter side is calledbreadth . We use the letter l and b to stand for the length and the breath.

perimeter of rectangle = l + b + l + b This formular can be use to
= (l + b) + (l + b) calculate the perimeter of
= 2 × (l + b) rectangle.
= 2(l + b)

Example
Calculate the perimeter of a football field which measures 80m by 50m.
Solution
Perimeter of field = 2(l+ b)
= 2 × (80 + 50) m
= 2 × 130m
= 260m.
(3) A rectangular piece of land measures 57 m by 42m. What is the perimeter of the perimeter of the land ?
Perimeter of land = 2(l+ b)
= 2(57+ 45)m
= 2× 99m
= 198m.
AREA OF A TRIANGLES
Any diagonal of a rectangle divided it into two equal right- angled triangles.


Thus :
Area of a right – angled triangle
= ½ × product of sides containing the right angle.
Area of triangle = ½ × base × height.
Example:
Calculate the area of the triangle shown below;

The two sides containing the right angle measure 9 cm and 12cm.
Area of triangle = ½ × 9cm × 12cm
= 54cm2
(2) calculate the area of the triangle with height 5cm, base 8cm and hypotenuse 7cm.
The height is 5cm. The corresponding base is 8cm. We do not need the 7 cm side.
Solution:
Area of triangle = ½ ×base × height
= ½ × 8cm × 5cm
= 20cm2
Evaluation:
New general mathematics for junior secondary schools 1 UBE Edition.
Exercise 14d 1(a) –(d) page 120.
AREA OF A TRAPEZIUMS:

ABCD is a trapezium in which AB is parallel to DC. The diagonal AD divides the trapezium into two triangles. The height, h, is the same for both triangles.
area of trapezium ABCD
= area of ABD + area of BDC
½ AB × h + ½ DC × h
= ½ (AB + DC)h
Example:
Calculate the area of the trapezium ABCD in figure below;
The diagonal AC divides the trapezium into two triangles. The height of each triangle is 8 cm.
Area of ACB = ½ × 13cm × 8cm =52cm2
Area of ACD = ½ × 6cm × 8cm = 24cm2
Area of trapezium = 52cm2 + 24cm2 =76cm2
Evaluation:
New general mathematics for junior secondary school 1 UBE Edition,
Exercise : 14d no’s: 2(a) – (d).
Area of parallelograms
A parallelogram can have two bases and two corresponding heights as show below;

Area (A) = base (1) × height (1)
Also area (A) =base(2) × height (2)
Therefore base (1) × height (2) × height (2)
Example:
Calculate the area of the paralellograms below. All dimensions are in centimeters.
base = 5
height = 7
(a) Area of parallelogram = base × height
= 7cm × 5 cm
= 35cm
base = 5
height = 3
(b) Area of parallelogram = base × height
= 5cm × 3cm
= 15cm.
Evaluation:
1. Calculate the area of a parallelogram if its base is 9.2cm and its height is 6cm
2. the area of a parallelogram is 99cm2 its base is 11cm. calculate the corresponding height of the parallogram
3. calculate the base of a parallelogram whose area and height is 27cm and 9cm respectively.
Area of a circles
Area of a circle = ∏r2
∏ = 22/7

Diameter= 2r. where r = radius
Example:
(1) Find the area of a circle whose radius is 3½m. Taken∏to be 22/7
Solution:
area of a circle = ∏r2
= 22/7 × (3½)2= 22/7 × 7/2 × 7/2m2
= 11 × 7
2
= 381/2 m2

Evaluation:
New general mathematics for junior secondary schools 1 UBE Edition . Exercise 14e 1(a)- (f) page 122. take ∏= 22/7
Reading assignment:
New general mathematics for junior secondary schools 1 UBE Edition. Page 116- 123.
assignment:
New general mathematics for junior secondary schools 1 UBE Edition. Page116 -123. Exercise 14e 3(a) –(f), Exercise 14d 1 (a) – (e).
WEEK 2
Topic : plane shapes : Perimeter of irregular shapes. Area of regular and irregular shapes, such as squares, rectangles, parallelograms,
Contents :
Perimeter of irregular shapes
Area of regular and irregular shapes
Perimeter of irregular shapes
The simplest way to find a perimeter irregular shape is to measure it directly with a ruler or tape measure.
Example ;
1. Measure the perimeter of the quadrilateral ABCD In the fig. below

By measurement, AB = 50mm = 5.0cm
BC = 25mm = 2.5cm
CD = 50mm = 5.0cm
DA = 25mm = 2.5cm
Perimeter =150mm = 150.0cm
AREA OF A SQUARE
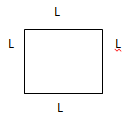
Perimeter of a square= 4L i.e L
L × L × L × L=4L
EXAMPLE:
Find the perimeter of a square whose side is 5cm.
Solution:
Formular for perimeter of a square = 4L
= 4× 5cm
=20cm.
Evaluation:
New general mathematics for junior secondary schools 1 UBE Edition.
Page 106 Exercise 13b no 2 : (a) –(l)
ASSIGNMENT
New general mathematics for junior secondary schools 1 UBE Edition.
Page 106 exercise 13b no: (a) – (o)
Topic : Three dimentional figures :
Content :
Basic properties of cubes an cuboids
Basic properties of yramids and cones
Basic properties of cylinders and spheres.
Basic properties of cubes and cuboids
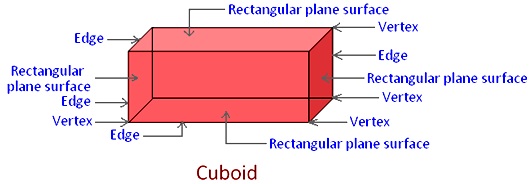
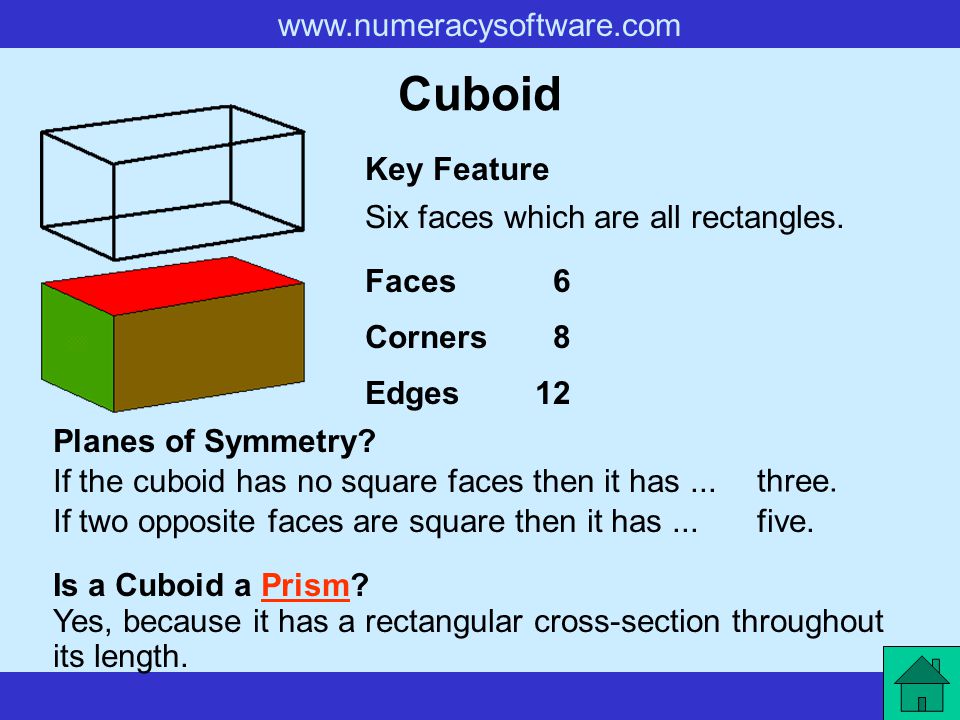
The cuboid is one of the most common manufactured solids. All solids have surfaces, or faces. Most solids also also have edges
A face may be flat (plane) or curved. A cuboid has 6 plane faces. Face is in the shape of a rectangle.

An edge is a line where two faces meet. it may be straight or curved. A cuboid has straight edges.
A vertex is a point or corner where three or more edges meet. The plural of vertex is vertices. A cuboid has 8 vertices.
Students should make a cuboid using a cardboard paper.
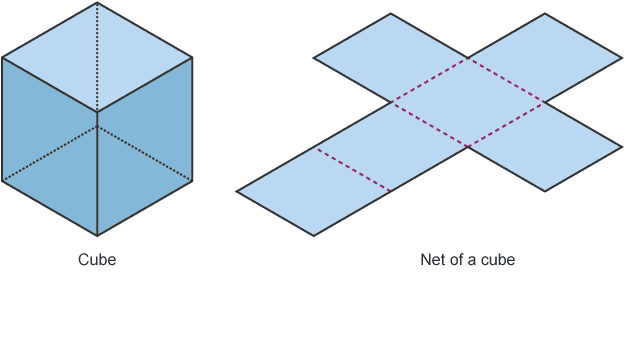
Cubes
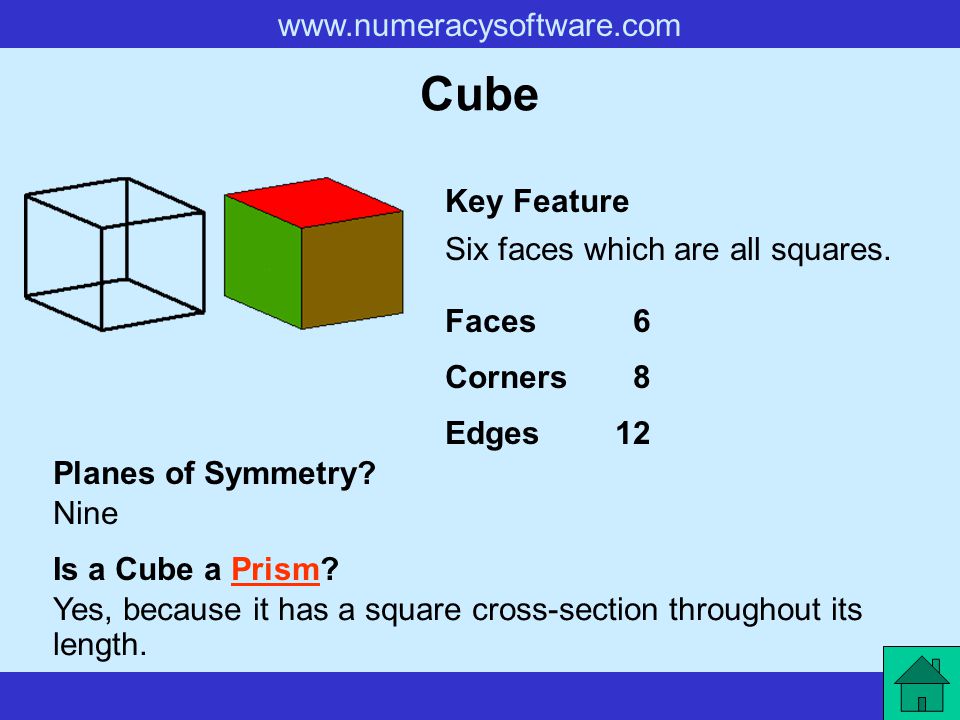
A cube is a cuboid in which all six faces are squares.
A cube & Net of a cube
Cones and pyramids
The root of the house is the cone. The base of a cone is a circle. The cone is quite a common shape but it is usually part of a bigger object .
Cylinders and prisms
The cylinder has two plane faces and one curved face. It has no vertices and two curved edges. The two plane faces are both circles .
Student should learn how to make cylinders and prisms practically using cardboard paper.
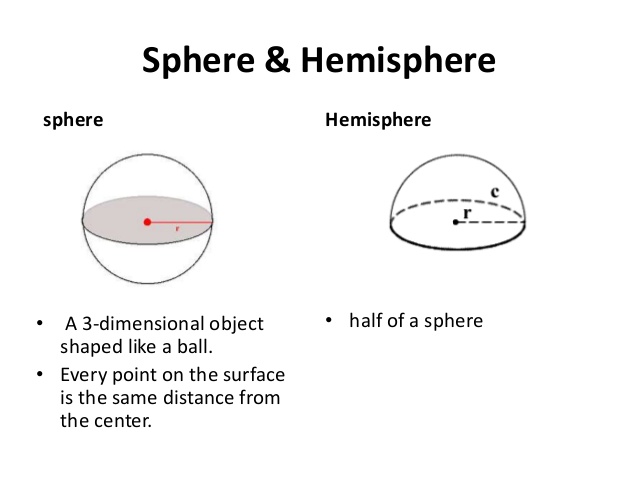
Sphere
Nearly every ball is sphere- shaped

Half a sphere is called a hemisphere
Evaluation:
New general mathematic for junior secondary schools for jss1 .
Page 48 Exercise 6b no: 1-6(a)-(f)., Exercise 6d no: 7, .
Assignment:
New general mathematic for junior secondary schools for jss 1.
Page 48 Exercise 6b no : 8, 9, & 10., Exercise 6e no : 1-4.
Contents :
Perimeter of irregular shapes
Area of regular and irregular shapes
Perimeter of irregular shapes
The simplest way to find a perimeter irregular shape is to measure it directly with a ruler or tape measure.
Example ;
1. Measure the perimeter of the quadrilateral ABCD In the fig. below

By measurement, AB = 50mm = 5.0cm
BC = 25mm = 2.5cm
CD = 50mm = 5.0cm
DA = 25mm = 2.5cm
Perimeter =150mm = 150.0cm
AREA OF A SQUARE

Perimeter of a square= 4L i.e L
L × L × L × L=4L
EXAMPLE:
Find the perimeter of a square whose side is 5cm.
Solution:
Formular for perimeter of a square = 4L
= 4× 5cm
=20cm.
Evaluation:
New general mathematics for junior secondary schools 1 UBE Edition.
Page 106 Exercise 13b no 2 : (a) –(l)
ASSIGNMENT
New general mathematics for junior secondary schools 1 UBE Edition.
Page 106 exercise 13b no: (a) – (o)
Topic : Three dimentional figures :
Content :
Basic properties of cubes an cuboids
Basic properties of yramids and cones
Basic properties of cylinders and spheres.
Basic properties of cubes and cuboids

The cuboid is one of the most common manufactured solids. All solids have surfaces, or faces. Most solids also also have edges
A face may be flat (plane) or curved. A cuboid has 6 plane faces. Face is in the shape of a rectangle.

An edge is a line where two faces meet. it may be straight or curved. A cuboid has straight edges.
A vertex is a point or corner where three or more edges meet. The plural of vertex is vertices. A cuboid has 8 vertices.
Students should make a cuboid using a cardboard paper.
Cubes
A cube is a cuboid in which all six faces are squares.
A cube & Net of a cube

Cones and pyramids

The root of the house is the cone. The base of a cone is a circle. The cone is quite a common shape but it is usually part of a bigger object .
Cylinders and prisms
The cylinder has two plane faces and one curved face. It has no vertices and two curved edges. The two plane faces are both circles .
Student should learn how to make cylinders and prisms practically using cardboard paper.
Sphere
Nearly every ball is sphere- shaped

Half a sphere is called a hemisphere

Evaluation:
New general mathematic for junior secondary schools for jss1 .
Page 48 Exercise 6b no: 1-6(a)-(f)., Exercise 6d no: 7, .
Assignment:
New general mathematic for junior secondary schools for jss 1.
Page 48 Exercise 6b no : 8, 9, & 10., Exercise 6e no : 1-4.
WEEK 3
TOPIC: Properties of Solid Shapes – Volume of cubes and cuboids
CONTENT:
3 – Dimensional shapes
Properties of solid shapes – cubes and cuboids
Volume of cubes and cuboids
3 – DIMENSIONAL SHAPES
Solid figures are often called 3 – dimensional shapes or 3 – D shapes. A solid figure is simply anything that occupies space and also has a definite shape. Most solids, or 3 – D shapes, such as stones and trees, have rough and irregular shapes. However, some solids, such as boxes, tins, football, etc. have regular shapes. These are often called geometrical solids.
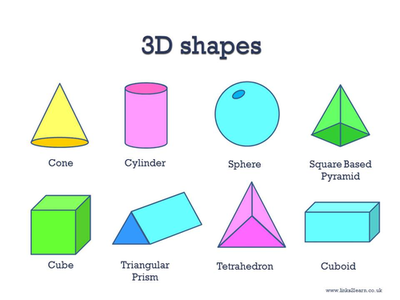
PROPERTIES OF SOLID SHAPES – CUBES AND CUBOIDS
A cube is a special cuboid which has all its edges equal in length (i.e all sides are equal). it has six square faces. Examples are: a cube of sugar, maggi cube, dice, etc.
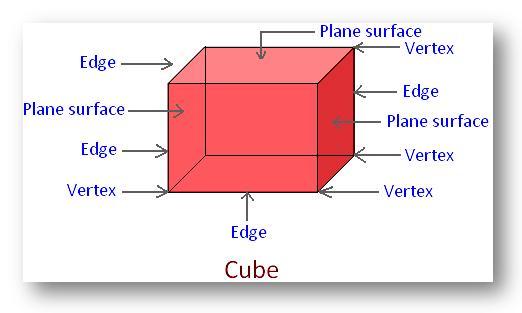
A cuboid is a solid shape with 6 rectangular faces. It also has 12 edges and 8 vertices. Examples are matchbox, carton, box of chalks, books, etc.
VOLUME OF CUBES AND CUBOIDS.
The volume of a solid is a measure of the amount of space it occupies. A solid object is called a 3 - dimensional object. The cube is used as the basic shape to estimate the volume of a solid. therefore, volume is measured in cubic units.
CUBES
If one edge of a cube is S unit long, then
Volume of a cube = side x side x side
i.e V = s x s x s
= S3
WORKED EXAMPLES
Calculate the volume of a cube of an edge 4cm.
Solution
Volume of a cube = length x height x width
= s x s x s
= 4 x 4 x 4
= 64cm3
NOTE: The above formula can be used to find the edge of a cube when the volume is given.
S3 = V
S = ∛V
e.g. A cube of volume of 27cm3 has an edge of
s = ∛s=∛27=∛(3 x 3 x 3) = 3cm
A container in the shape of a cube is used to store a liquid. One edge of the container is 25cm long. The depth of the liquid in the container is 15cm as shown in the diagram below.
calculate the volume of liquid in the container
calculate the volume of the container not filled with liquid.
Solution
Base area of the container = 25 x 25
= 625cm2
Depth of liquid in the container = 15cm
Volume of liquid in the container = 625 x 15 = 9375cm3
Volume of the cube = S3 = 25 x 25 x 25
= 15 625cm3
Volume of the container not filled liquid
= 15 625 – 9 375
= 6 250cm3

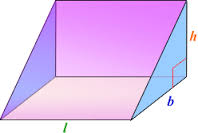
CUBOIDS
A cuboid is also called a rectangular prism. It has length, width (breadth) and height (thickness).
The volume of a cuboid = length x breadth x height
V = l x b x h
The volume of the above solid is
V = 6 x 4 x 2 = 48cm3
Note: In the above formula, l x b = A. Where A = base area of the cuboid.
Hence: Volume of a cuboid = Area of base x height
= Area of any face x thickness of the face.
WORKED EXAMPLES
A box has a square base of side 9cm. Calculate the volume of the box if it is 10cm deep.
Solution
Volume of the box = Area of Square base x depth of the box
Area of Square base = 9cm x 9cm
= 81cm2
Volume of the box = 81 x 10
= 810cm3
A cuboid is 12cm long and 8cm wide as shown in the diagram below. If the volume of cuboid is 624cm3, find the height of the cuboid.
v = 624cm3
h
8cm
12cm
Solution
length x width x height = volume
i.e l x w x h = V
Substituting V =624cm3, l = 12cm and w = 8cm
12 x 8 x h = 624
96h = 624
h = 624/96 = 6.5cm
Hence, the height of the cuboid = 6.5cm.

EVALUATION:
A book measures 18cm by 12cm by 3cm. Calculate its volume.
The volume of a cube is given as 512cm3
What is the length of one edge of the cube?
How many small cubes of edge 2cm can be placed together to make this cube?
The base of a cuboid has one side equal to 10cm, and the other side is 5cm longer. If the height of the cuboid is 7cm, find the volume of the cuboid.
Calculate the volume of air in a dormitory 10cm long, 5m wide and 3m high.
READING ASSIGNMENT:
New General Mathematics JS1 (UBE Edition), Page 44 to 45 and page 130 to 133
ASSIGNMENT:
New General Mathematics JS1 (UBE Edition), Ex. 16a. Q 1(a-j), Q7, Q12 and Q13 Page .
CONTENT:
3 – Dimensional shapes
Properties of solid shapes – cubes and cuboids
Volume of cubes and cuboids
3 – DIMENSIONAL SHAPES
Solid figures are often called 3 – dimensional shapes or 3 – D shapes. A solid figure is simply anything that occupies space and also has a definite shape. Most solids, or 3 – D shapes, such as stones and trees, have rough and irregular shapes. However, some solids, such as boxes, tins, football, etc. have regular shapes. These are often called geometrical solids.

PROPERTIES OF SOLID SHAPES – CUBES AND CUBOIDS
A cube is a special cuboid which has all its edges equal in length (i.e all sides are equal). it has six square faces. Examples are: a cube of sugar, maggi cube, dice, etc.


A cuboid is a solid shape with 6 rectangular faces. It also has 12 edges and 8 vertices. Examples are matchbox, carton, box of chalks, books, etc.

VOLUME OF CUBES AND CUBOIDS.
The volume of a solid is a measure of the amount of space it occupies. A solid object is called a 3 - dimensional object. The cube is used as the basic shape to estimate the volume of a solid. therefore, volume is measured in cubic units.
CUBES
If one edge of a cube is S unit long, then
Volume of a cube = side x side x side
i.e V = s x s x s
= S3
WORKED EXAMPLES
Calculate the volume of a cube of an edge 4cm.
Solution
Volume of a cube = length x height x width
= s x s x s
= 4 x 4 x 4
= 64cm3
NOTE: The above formula can be used to find the edge of a cube when the volume is given.
S3 = V
S = ∛V
e.g. A cube of volume of 27cm3 has an edge of
s = ∛s=∛27=∛(3 x 3 x 3) = 3cm
A container in the shape of a cube is used to store a liquid. One edge of the container is 25cm long. The depth of the liquid in the container is 15cm as shown in the diagram below.
calculate the volume of liquid in the container
calculate the volume of the container not filled with liquid.
Solution
Base area of the container = 25 x 25
= 625cm2
Depth of liquid in the container = 15cm
Volume of liquid in the container = 625 x 15 = 9375cm3
Volume of the cube = S3 = 25 x 25 x 25
= 15 625cm3
Volume of the container not filled liquid
= 15 625 – 9 375
= 6 250cm3

CUBOIDS
A cuboid is also called a rectangular prism. It has length, width (breadth) and height (thickness).
The volume of a cuboid = length x breadth x height
V = l x b x h
The volume of the above solid is
V = 6 x 4 x 2 = 48cm3
Note: In the above formula, l x b = A. Where A = base area of the cuboid.
Hence: Volume of a cuboid = Area of base x height
= Area of any face x thickness of the face.
WORKED EXAMPLES
A box has a square base of side 9cm. Calculate the volume of the box if it is 10cm deep.
Solution
Volume of the box = Area of Square base x depth of the box
Area of Square base = 9cm x 9cm
= 81cm2
Volume of the box = 81 x 10
= 810cm3
A cuboid is 12cm long and 8cm wide as shown in the diagram below. If the volume of cuboid is 624cm3, find the height of the cuboid.
v = 624cm3
h
8cm
12cm
Solution
length x width x height = volume
i.e l x w x h = V
Substituting V =624cm3, l = 12cm and w = 8cm
12 x 8 x h = 624
96h = 624
h = 624/96 = 6.5cm
Hence, the height of the cuboid = 6.5cm.

EVALUATION:
A book measures 18cm by 12cm by 3cm. Calculate its volume.
The volume of a cube is given as 512cm3
What is the length of one edge of the cube?
How many small cubes of edge 2cm can be placed together to make this cube?
The base of a cuboid has one side equal to 10cm, and the other side is 5cm longer. If the height of the cuboid is 7cm, find the volume of the cuboid.
Calculate the volume of air in a dormitory 10cm long, 5m wide and 3m high.
READING ASSIGNMENT:
New General Mathematics JS1 (UBE Edition), Page 44 to 45 and page 130 to 133
ASSIGNMENT:
New General Mathematics JS1 (UBE Edition), Ex. 16a. Q 1(a-j), Q7, Q12 and Q13 Page .
WEEK 4
TOPIC: VOLUME OF RIGHT-ANGLED TRIANGULAR PRISM
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to calculate the volume of right-angled triangular prisms

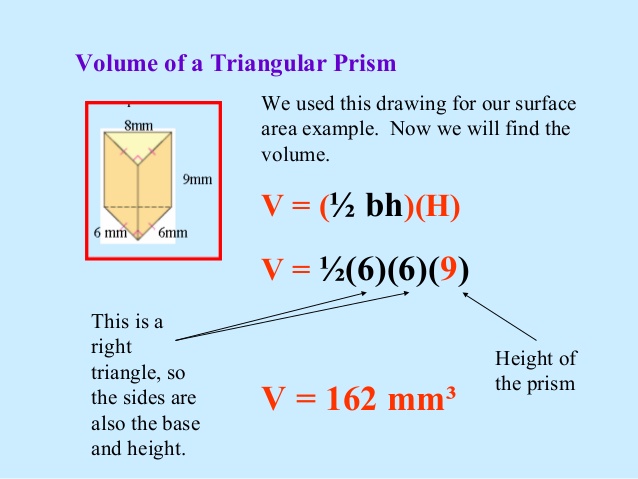
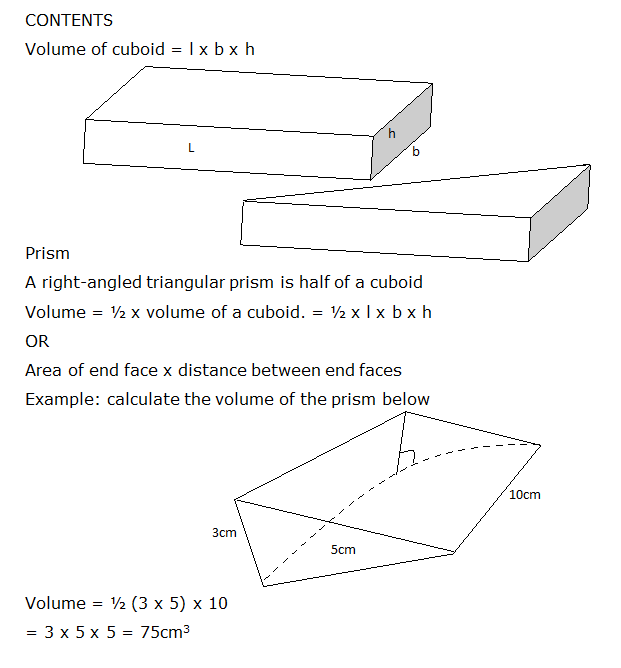
view content below
https://skydrive.live.com/?cid=99bc2c15 ... 2A33%21153
EVALUATION
New general maths for JSS1, page 134 Exercise 16c: Questions 1, 2 and 3
further studies / practice test
http://www.mathsteacher.com.au/year9/ch ... /prism.htm
http://www.skwirk.com.au/p-c_s-12_u-214 ... face-area/
watch video
http://www.videojug.com/film/how-to-fin ... ular-prism
LESSON 83
TOPIC: Finding the height of right-angled triangular prism.
PERFORMANCE OBJECTIVE: At the end of the lesson, students should be able to calculate the height of triangular prism give the area of end-face and the volume
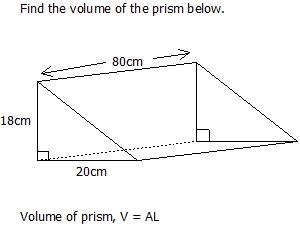
CONTENTS
Area of end face x height = volume of ∆ or prisms.
:. Height =
Example: the volume of a triangular prism is 60cm3. If the area of end-face is 6cm2, calculate its height.
Volume = 60cm3 ; Area = 6cm2; height =?
Height = = = 10cm

EVALUATION
a. If the volume of right-angled triangular prism is 35cm3 and the area of end-face is 5cm2, what is the height?
b. The volume of a right-angled triangular prism is 90cm3; if the area of end-face is 7.5cm2.find the height of the prism.
ASSIGNMENT: New general Maths for JSS1, page 134; Ex 16c. questions 5 and 6
further studies
http://www.purplehell.com/riddletools/maths.htm
http://metal.brightcookie.com/1_calc/ca ... 2_2_8c.htm
practice test
http://www.funtrivia.com/playquiz/quiz1 ... d9bc0.html
watch video
http://www.funtrivia.com/flashquiz/index.cfm?qid=147129
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to calculate the volume of right-angled triangular prisms



view content below
https://skydrive.live.com/?cid=99bc2c15 ... 2A33%21153

EVALUATION
New general maths for JSS1, page 134 Exercise 16c: Questions 1, 2 and 3
further studies / practice test
http://www.mathsteacher.com.au/year9/ch ... /prism.htm
http://www.skwirk.com.au/p-c_s-12_u-214 ... face-area/
watch video
http://www.videojug.com/film/how-to-fin ... ular-prism
LESSON 83
TOPIC: Finding the height of right-angled triangular prism.
PERFORMANCE OBJECTIVE: At the end of the lesson, students should be able to calculate the height of triangular prism give the area of end-face and the volume

CONTENTS
Area of end face x height = volume of ∆ or prisms.
:. Height =
Example: the volume of a triangular prism is 60cm3. If the area of end-face is 6cm2, calculate its height.
Volume = 60cm3 ; Area = 6cm2; height =?
Height = = = 10cm

EVALUATION
a. If the volume of right-angled triangular prism is 35cm3 and the area of end-face is 5cm2, what is the height?
b. The volume of a right-angled triangular prism is 90cm3; if the area of end-face is 7.5cm2.find the height of the prism.
ASSIGNMENT: New general Maths for JSS1, page 134; Ex 16c. questions 5 and 6
further studies
http://www.purplehell.com/riddletools/maths.htm
http://metal.brightcookie.com/1_calc/ca ... 2_2_8c.htm
practice test
http://www.funtrivia.com/playquiz/quiz1 ... d9bc0.html
watch video
http://www.funtrivia.com/flashquiz/index.cfm?qid=147129
WEEK 5
MAIN TOPIC: Properties /identification of angles
SPECIFIC TOPIC: Angles between lines or straight angles
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to calculate the size of angles on straight lines
REFERENCE BOOK: New general maths for JSS1 page 156
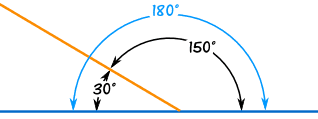
View content below
https://skydrive.live.com/?cid=99bc2c15 ... 2A33%21151
Assignment
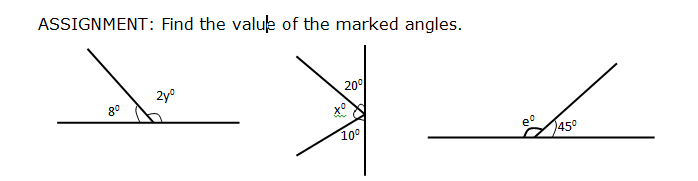
further studies
http://www.mathsteacher.com.au/year7/ch ... ng/ang.htm
http://www.netcomuk.co.uk/~jenolive/vect14.html
http://www.mathsisfun.com/angles.html
practice test
http://www.math10.com/en/tests/angles/angles-test.html
watch video
[youtube]http://www.youtube.com/watch?v=NpVZWtFk ... re=related[/youtube]
LESSON 85
TOPIC: Vertically Opposite Angles
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to identify and calculate the size of vertically opposite angles
View content below
https://skydrive.live.com/?cid=99bc2c15 ... 2A33%21150
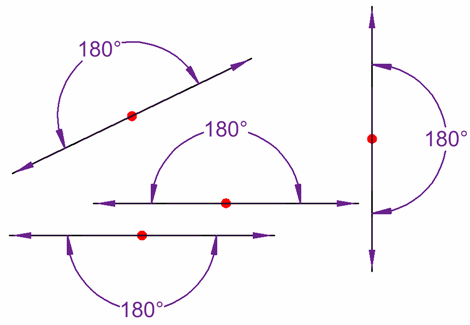
ASSIGNMENT: New general maths for JSS1 page 159 Ex. 20c, numbers 2,3 and 4
further studies
http://www.mathsisfun.com/geometry/parallel-lines.html
http://www.mathsisfun.com/geometry/vert ... ngles.html
http://www.mathsteacher.com.au/year7/ch ... rt/opp.htm
practice test
http://www.studyzone.org/mtestprep/math ... nglesl.cfm
watch video
[youtube]http://www.youtube.com/watch?v=h7TYeYRM-xY[/youtube]
LESSON 86
TOPIC: Angles meeting at a point
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to identify and calculate the size of angles meeting at a point

View content below

further studies
http://www.mathsisfun.com/angle360.html
practice test
http://www.cimt.plymouth.ac.uk/projects ... k7_5i4.htm
http://cuip.uchicago.edu/wit/99/teams/g ... yquiz3.htm
http://www.ixl.com/math/grade-7/paralle ... tersecting
watch video
[youtube]http://www.youtube.com/watch?v=n1yQVYBktEM[/youtube]
LESSON 87
TOPIC: Parallel lines /corresponding angles
PERFORMANCE OBJECTIVE: At the end of the lesson, students should be able to:
a. Identify parallel lines
b. Calculate the size of angles between parallel lines
View content below
https://skydrive.live.com/?cid=99bc2c15 ... 2A33%21148
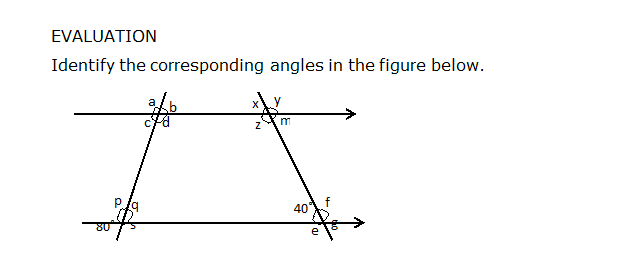
ASSIGNMENT: New general maths for JSS1 page 162, questions 1 and 2
further studies
http://www.ies.co.jp/math/products/geo1 ... kuhei.html
http://www.mathsisfun.com/geometry/corr ... ngles.html
http://www.mathwarehouse.com/geometry/a ... angles.php
practice test
http://www.thatquiz.org/tq/practicetest?4z8qgnzp2o
watch video
[youtube]http://www.youtube.com/watch?v=-6jjmL3JYts[/youtube]
SPECIFIC TOPIC: Angles between lines or straight angles
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to calculate the size of angles on straight lines
REFERENCE BOOK: New general maths for JSS1 page 156

View content below

https://skydrive.live.com/?cid=99bc2c15 ... 2A33%21151
Assignment
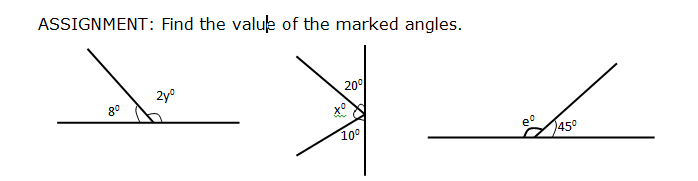
further studies
http://www.mathsteacher.com.au/year7/ch ... ng/ang.htm
http://www.netcomuk.co.uk/~jenolive/vect14.html
http://www.mathsisfun.com/angles.html
practice test
http://www.math10.com/en/tests/angles/angles-test.html
watch video
[youtube]http://www.youtube.com/watch?v=NpVZWtFk ... re=related[/youtube]
LESSON 85
TOPIC: Vertically Opposite Angles
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to identify and calculate the size of vertically opposite angles
View content below

https://skydrive.live.com/?cid=99bc2c15 ... 2A33%21150

ASSIGNMENT: New general maths for JSS1 page 159 Ex. 20c, numbers 2,3 and 4
further studies
http://www.mathsisfun.com/geometry/parallel-lines.html
http://www.mathsisfun.com/geometry/vert ... ngles.html
http://www.mathsteacher.com.au/year7/ch ... rt/opp.htm
practice test
http://www.studyzone.org/mtestprep/math ... nglesl.cfm
watch video
[youtube]http://www.youtube.com/watch?v=h7TYeYRM-xY[/youtube]
LESSON 86
TOPIC: Angles meeting at a point
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to identify and calculate the size of angles meeting at a point

View content below


further studies
http://www.mathsisfun.com/angle360.html
practice test
http://www.cimt.plymouth.ac.uk/projects ... k7_5i4.htm
http://cuip.uchicago.edu/wit/99/teams/g ... yquiz3.htm
http://www.ixl.com/math/grade-7/paralle ... tersecting
watch video
[youtube]http://www.youtube.com/watch?v=n1yQVYBktEM[/youtube]
LESSON 87
TOPIC: Parallel lines /corresponding angles
PERFORMANCE OBJECTIVE: At the end of the lesson, students should be able to:
a. Identify parallel lines
b. Calculate the size of angles between parallel lines

View content below

https://skydrive.live.com/?cid=99bc2c15 ... 2A33%21148

ASSIGNMENT: New general maths for JSS1 page 162, questions 1 and 2
further studies
http://www.ies.co.jp/math/products/geo1 ... kuhei.html
http://www.mathsisfun.com/geometry/corr ... ngles.html
http://www.mathwarehouse.com/geometry/a ... angles.php
practice test
http://www.thatquiz.org/tq/practicetest?4z8qgnzp2o
watch video
[youtube]http://www.youtube.com/watch?v=-6jjmL3JYts[/youtube]
WEEK 6
MAIN TOPIC: CONSTRUCTION
SPECIFIC TOPIC: PARALLEL LINES
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to construct parallel lines.
REFERENCE BOOK: New general maths for West Africa (JSS 1)
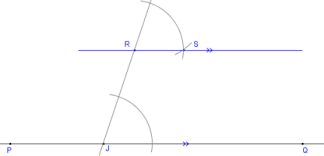
CONTENTS
Example: construct a line through P so that it is parallel to AB
a. Place a set square so that on edge is accurately along AB
b. Place a ruler along one of the other edges of the set square
c. Hold the ruler firmly. Slide the set square along the ruler towards P. draw a line along the edge of the set square through P.
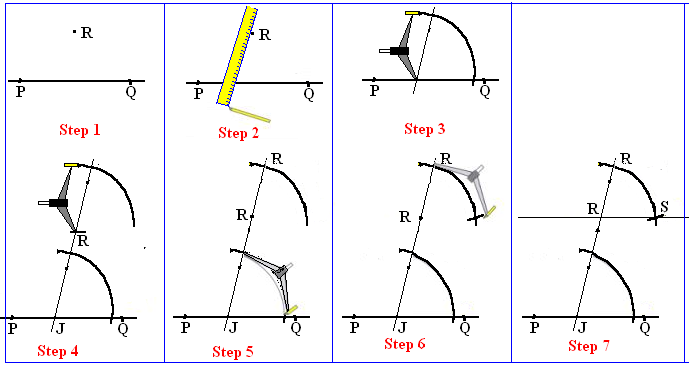
EVALUATION
Draw a straight line AB on a piece of paper. Construct a line through P so that it is parallel to AB.
ASSIGNMENT
Use a ruler and a set square to draw four lines that are parallel to one another
further studies
http://www.mathsisfun.com/geometry/constructions.html
http://www.hstutorials.net/math/geometr ... n_line.htm
http://www.mathopenref.com/constparallel.html
practice test
http://soowook.com/home/geometry/
LESSON 89
TOPIC: CONSTRUCTION OF PARALLELOGRAMS
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to construct parallelogram using rulers and a set squares
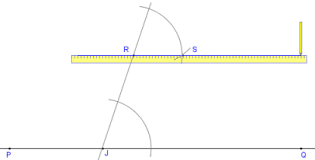
CONTENTS
Example: Draw angle ABC = 500 so that the arms BA and BC are 4cm and 5cm long.
b. Draw a line through A parallel to BC
c. Draw a line through C parallel to BA to make parallelogram ABCD
d. Measure the four sides of the parallelogram.
EVALUATION
Construct a parallelogram ABCD with AB = 3cm, BC = 4cm and
B=750 Draw the diagonals AC and BD to intersect at point X.
ASSIGNMENT: New general maths for JSS 1 page 167, questions 9a and b
further studies
http://www.scribd.com/examville/d/11579 ... allelogram
practice test
http://www.youtube.com/watch?v=-LRrj52j ... re=related
LESSON 90
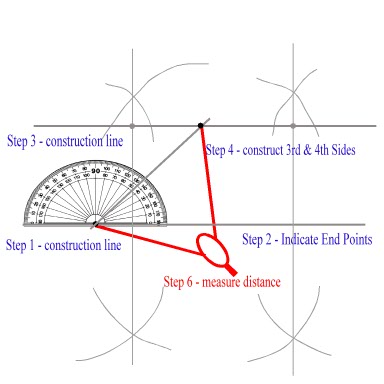
TOPIC: Constructing perpendicular lines
PERFORMANCE OBJECTIVE: At the end of the lesson, students should be able to construct perpendicular lines
CONTENTS
Two lines that meet at right angles are called perpendicular lines
Line CD is ar to AB
Example: Construct a perpendicular line from point P on a line l
a. Placer a ruler along the given line
b. Use the two edges of the set square which contain its right angle
c. Place one of these edges along the ruler
d. Slide down the set square along the ruler until the other edge reaches P
e. Draw a line through P perpendicular to l
EVALUATION: New general maths for JSS 1 page 169; Ex 21b questions 1a and b
ASSIGNMENT: Page 169. Ex 21b question 2a and 2b
further studies
http://www.mathopenref.com/constperpextpoint.html
http://www.mathopenref.com/constperplinepoint.html
http://www.mathopenref.com/constbisectline.html
practice test
http://www.phschool.com/webcodes10/inde ... uffix=0304
TOPIC: CONSTRUCTION
CONTENT:
Construction of parallel lines
Construction of perpendicular lines.
Measurement of angles.
Construction
To construct a figure in geometry implies to draw it accurately. The proper use of measuring and drawing instruments such as protractor, ruler, set square, pencil, etc will enhance accurate construction.
NOTE:
Always make a rough sketch of what you are going to draw before starting construction questions.
The teacher should introduce all the instrument of geometric construction to the students and students should be able to indentify each and know their uses.
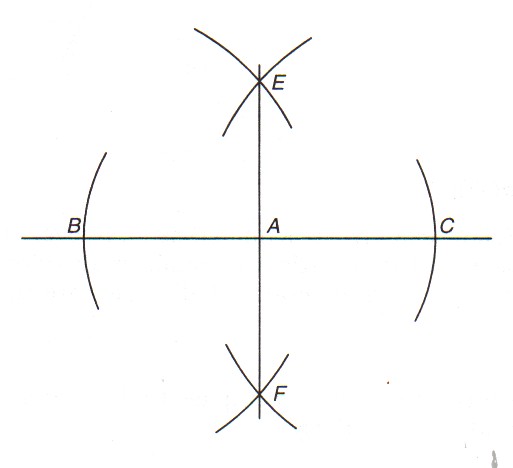
CONSTRUCTION OF PARALLEL LINES
Parallel lines are lines that do not meet. They always have the same distance apart and are in the same direction.

b. Place a ruler along one of the other edges of the set square as shown in the diagram.
c. Hold the ruler firmly with one hand and then slide the set -square with the second hand along the edge of the ruler until you reach point O.
d. Draw the line with a sharp pencil.
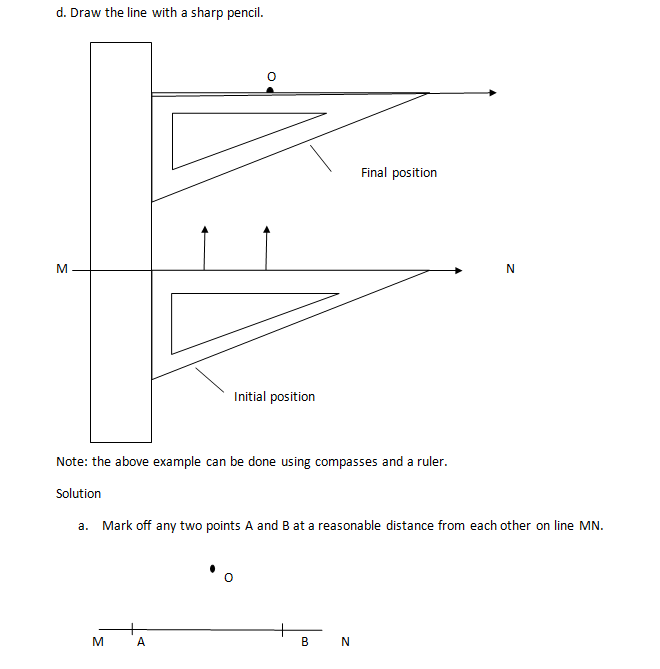
Note: the above example can be done using compasses and a ruler.
Solution
Mark off any two points A and B at a reasonable distance from each other on line MN.
b. Open the compasses to radius AB. Then, place the compasses at O and draw an arc above B.
c. Open the compasses to radius AO. Then, place the compasses at B and draw an arc to cut the first one at P.
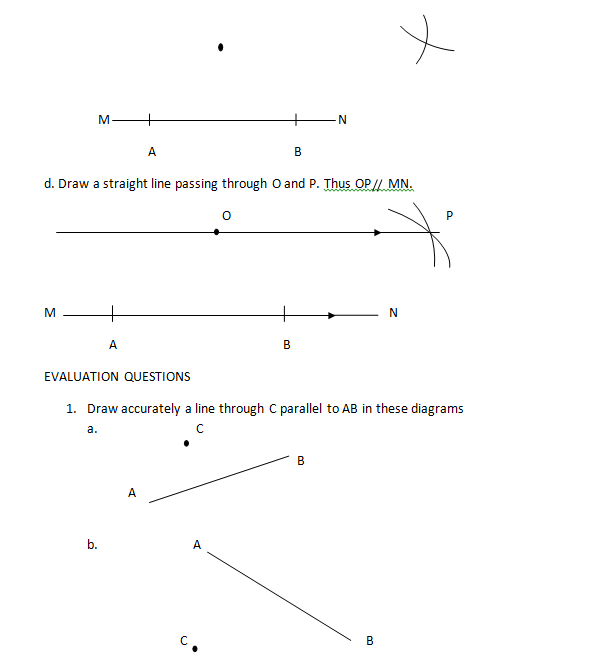
EVALUATION QUESTIONS
Draw accurately a line through C parallel to AB in these diagrams
Draw lines parallel to each of the following lines using the given distances.
RS = 7 cm, 4cm apart
EF = 6.5 cm , 3 cm apart.
CONSTRUCTION OF PERPENDICULAR LINES
Two lines are said to be perpendicular to each other if they intersect at right angles (i.e. 90 )
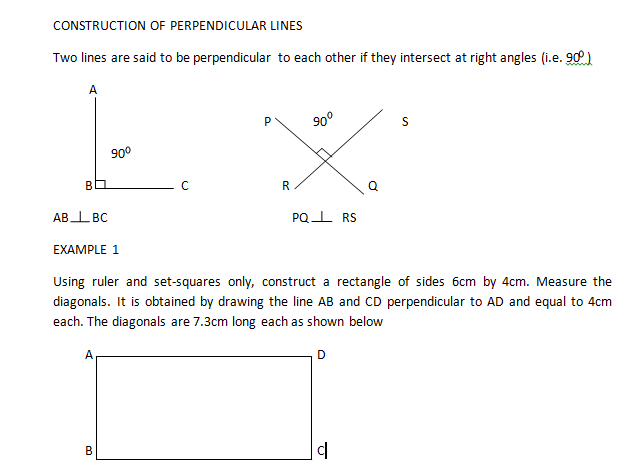
EXAMPLE 1
Using ruler and set-squares only, construct a rectangle of sides 6cm by 4cm. Measure the diagonals. It is obtained by drawing the line AB and CD perpendicular to AD and equal to 4cm each. The diagonals are 7.3cm long each as shown below
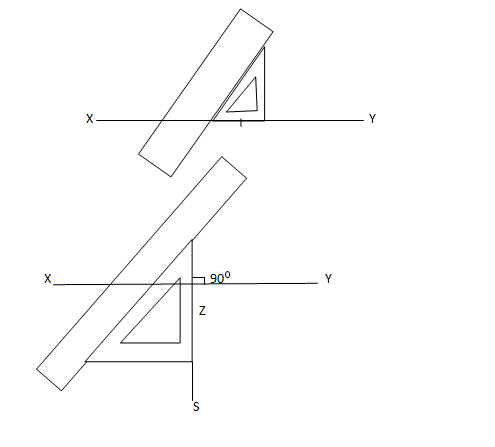
TO DRAW A PERPENDICULAR LINE FROM A POINT ON A LINE
Place one edge of the right angle of the set-square along the given line (i.e. XY).
Place a ruler along the hypotenuse as shown below.
Hold the ruler firmly with one hand and then slide the set-square with the second hand along the edge of the ruler until the required position Z is reached as shown in the diagram below. Then draw a line through R.
TO CONSTRUCT A PERPENDICULAR TO A LINE FROM A POINT OUTSIDE THE LINE
To draw a line through O perpendicular to XY in the diagram below
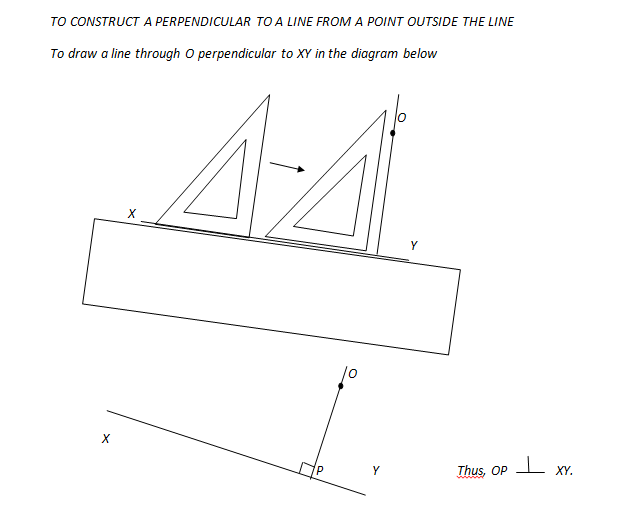
Place a ruler along line XY.
Place one edge of the right angle of the set-square along XY.
Hold the ruler firmly and then slide the set-square along the ruler until the vertical edge reaches the point O.
Hold the set-square firmly and use a pencil to draw a line through O to meet XY at P.
EVALUATION QUESTIONS
Draw a line RS = 6cm.
Mark three points A, B and C at the same distance apart on the line.
Using a ruler and set-square, draw a perpendicular to the line RS at each of these points.
What do you notice about the three lines?
a. Construct a rhombus of sides 5cm with an obtuse angle of size 100 degrees .
b .Measure the diagonals and the angles between them. What do you notice?
MEASUREMENT OF ANGLES
The protractor is a mathematical instrument used for measuring and drawing angles.
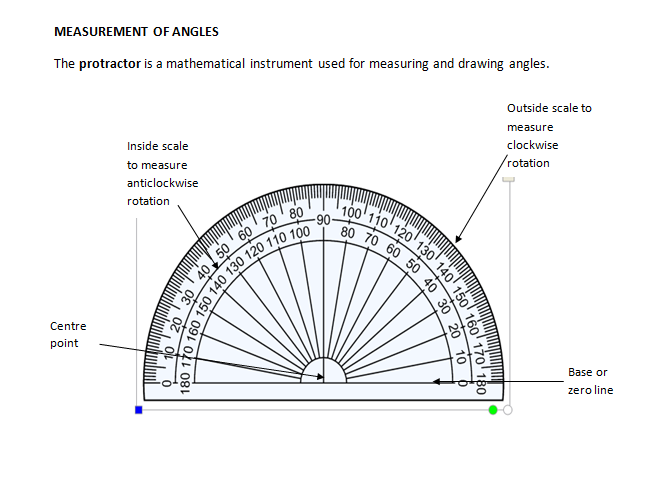
A protractor may be semicircular (i.e. 180 protractor) or circular (i.e. 360 protractor)in shape. There are two type of scales shown on a protractor, one is clockwise scalve and the other is anticlockwise scale as shown above.
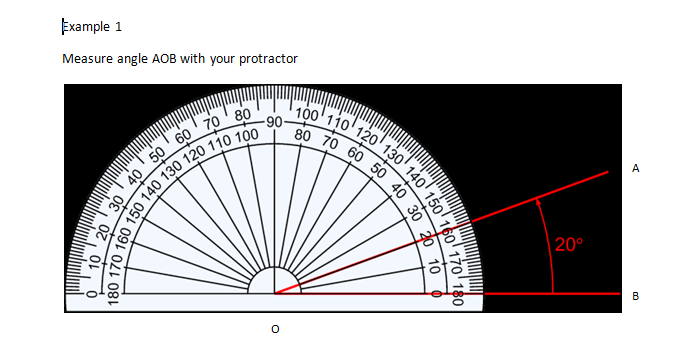
Example 1
Measure angle AOB with your protractor
Reading Assignment: New General Mathematics for Junior Secondary Schools 1
Pages 166 – 169.
Week-end Assignment: Ex. 21a, no 1 – 4 and Ex. 21b no 1, 4, 5 and 6
SPECIFIC TOPIC: PARALLEL LINES
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to construct parallel lines.
REFERENCE BOOK: New general maths for West Africa (JSS 1)

CONTENTS
Example: construct a line through P so that it is parallel to AB
a. Place a set square so that on edge is accurately along AB
b. Place a ruler along one of the other edges of the set square
c. Hold the ruler firmly. Slide the set square along the ruler towards P. draw a line along the edge of the set square through P.

EVALUATION
Draw a straight line AB on a piece of paper. Construct a line through P so that it is parallel to AB.
ASSIGNMENT
Use a ruler and a set square to draw four lines that are parallel to one another
further studies
http://www.mathsisfun.com/geometry/constructions.html
http://www.hstutorials.net/math/geometr ... n_line.htm
http://www.mathopenref.com/constparallel.html
practice test
http://soowook.com/home/geometry/
LESSON 89
TOPIC: CONSTRUCTION OF PARALLELOGRAMS
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to construct parallelogram using rulers and a set squares

CONTENTS
Example: Draw angle ABC = 500 so that the arms BA and BC are 4cm and 5cm long.
b. Draw a line through A parallel to BC
c. Draw a line through C parallel to BA to make parallelogram ABCD
d. Measure the four sides of the parallelogram.

EVALUATION
Construct a parallelogram ABCD with AB = 3cm, BC = 4cm and
B=750 Draw the diagonals AC and BD to intersect at point X.
ASSIGNMENT: New general maths for JSS 1 page 167, questions 9a and b
further studies
http://www.scribd.com/examville/d/11579 ... allelogram
practice test
http://www.youtube.com/watch?v=-LRrj52j ... re=related
LESSON 90
TOPIC: Constructing perpendicular lines
PERFORMANCE OBJECTIVE: At the end of the lesson, students should be able to construct perpendicular lines

CONTENTS
Two lines that meet at right angles are called perpendicular lines
Line CD is ar to AB
Example: Construct a perpendicular line from point P on a line l
a. Placer a ruler along the given line
b. Use the two edges of the set square which contain its right angle
c. Place one of these edges along the ruler
d. Slide down the set square along the ruler until the other edge reaches P
e. Draw a line through P perpendicular to l
EVALUATION: New general maths for JSS 1 page 169; Ex 21b questions 1a and b
ASSIGNMENT: Page 169. Ex 21b question 2a and 2b
further studies
http://www.mathopenref.com/constperpextpoint.html
http://www.mathopenref.com/constperplinepoint.html
http://www.mathopenref.com/constbisectline.html
practice test
http://www.phschool.com/webcodes10/inde ... uffix=0304
TOPIC: CONSTRUCTION
CONTENT:
Construction of parallel lines
Construction of perpendicular lines.
Measurement of angles.
Construction
To construct a figure in geometry implies to draw it accurately. The proper use of measuring and drawing instruments such as protractor, ruler, set square, pencil, etc will enhance accurate construction.
NOTE:
Always make a rough sketch of what you are going to draw before starting construction questions.
The teacher should introduce all the instrument of geometric construction to the students and students should be able to indentify each and know their uses.
CONSTRUCTION OF PARALLEL LINES
Parallel lines are lines that do not meet. They always have the same distance apart and are in the same direction.

b. Place a ruler along one of the other edges of the set square as shown in the diagram.
c. Hold the ruler firmly with one hand and then slide the set -square with the second hand along the edge of the ruler until you reach point O.
d. Draw the line with a sharp pencil.

Note: the above example can be done using compasses and a ruler.
Solution
Mark off any two points A and B at a reasonable distance from each other on line MN.
b. Open the compasses to radius AB. Then, place the compasses at O and draw an arc above B.
c. Open the compasses to radius AO. Then, place the compasses at B and draw an arc to cut the first one at P.

EVALUATION QUESTIONS
Draw accurately a line through C parallel to AB in these diagrams
Draw lines parallel to each of the following lines using the given distances.
RS = 7 cm, 4cm apart
EF = 6.5 cm , 3 cm apart.
CONSTRUCTION OF PERPENDICULAR LINES
Two lines are said to be perpendicular to each other if they intersect at right angles (i.e. 90 )

EXAMPLE 1
Using ruler and set-squares only, construct a rectangle of sides 6cm by 4cm. Measure the diagonals. It is obtained by drawing the line AB and CD perpendicular to AD and equal to 4cm each. The diagonals are 7.3cm long each as shown below
TO DRAW A PERPENDICULAR LINE FROM A POINT ON A LINE
Place one edge of the right angle of the set-square along the given line (i.e. XY).
Place a ruler along the hypotenuse as shown below.
Hold the ruler firmly with one hand and then slide the set-square with the second hand along the edge of the ruler until the required position Z is reached as shown in the diagram below. Then draw a line through R.

TO CONSTRUCT A PERPENDICULAR TO A LINE FROM A POINT OUTSIDE THE LINE
To draw a line through O perpendicular to XY in the diagram below

Place a ruler along line XY.
Place one edge of the right angle of the set-square along XY.
Hold the ruler firmly and then slide the set-square along the ruler until the vertical edge reaches the point O.
Hold the set-square firmly and use a pencil to draw a line through O to meet XY at P.
EVALUATION QUESTIONS
Draw a line RS = 6cm.
Mark three points A, B and C at the same distance apart on the line.
Using a ruler and set-square, draw a perpendicular to the line RS at each of these points.
What do you notice about the three lines?
a. Construct a rhombus of sides 5cm with an obtuse angle of size 100 degrees .
b .Measure the diagonals and the angles between them. What do you notice?
MEASUREMENT OF ANGLES
The protractor is a mathematical instrument used for measuring and drawing angles.

A protractor may be semicircular (i.e. 180 protractor) or circular (i.e. 360 protractor)in shape. There are two type of scales shown on a protractor, one is clockwise scalve and the other is anticlockwise scale as shown above.
Example 1
Measure angle AOB with your protractor

Reading Assignment: New General Mathematics for Junior Secondary Schools 1
Pages 166 – 169.
Week-end Assignment: Ex. 21a, no 1 – 4 and Ex. 21b no 1, 4, 5 and 6
WEEK 7
TOPIC: CONSTRUCTING A RHOMBUS
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to construct a rhombus using rulers set squares and protractors.

CONTENTS
A rhombus is a parallelogram with all its sides the same length
Example: construct a rhombus with one angle of 450 and each side 4cm long
Rough sketch
Steps
1. Draw angle ABC = 450 so that arms BA and BC are 4cm each
2. Draw a line through C parallel to BA to make the rhombus ABCD
EVALUATION
a. Construct a rhombus with one angle of 650 and each side 4cm long.
b. Measure the angle between the diagonals
ASSIGNMENT
Construct a trapezium ABCD so that BC=6cm AB=3cm B=80 degrees and C= 70 degrees
further studies
http://mathandmultimedia.com/2011/01/09 ... 7-rhombus/
http://www.mathopenref.com/constangle30.html
watch video
http://www.youtube.com/watch?v=Gwkf_Fem2XI
LESSON 92
MAIN TOPIC: STATISTICS
SPECIFIC TOPIC: TYPES OF STATISTICAL PRESENTATION
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to interpret statistical data numerically and graphically
REFERENCE BOOK: New general maths for West Africa (JSS1) page 144
CONTENTS
Types of presentation
Data can be presented in the following ways:
a. Rank order list
b. Frequency table


c. Histogram
d. Bar chart
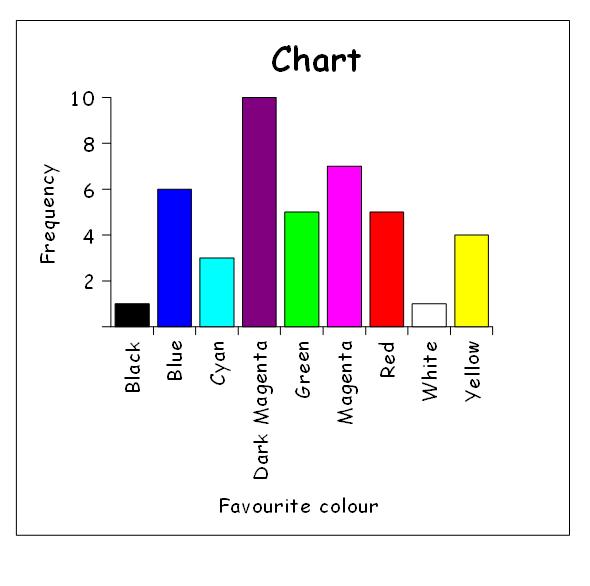
e. Pie chart
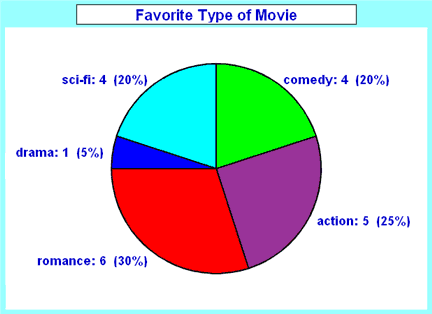
Example: An English teacher gave an essay to 15 students
She graded the essays from A (very good) through B, C, D, E, F (very poor) the grades of the students were: B, C,A,B,A,D,F,E,C,C,A,B,B,E,B
EVALUATION: (Oral)
New general maths for West Africa (JSS 1) page 145, Ex 18a. question 1,2,4,5
ASSIGNMENT: (Written)
New general maths for West Africa (JSS 1) page 147; exercise 18b question 11 and 12
further studies
http://www.scribd.com/doc/47650615/Stat ... tion-Tools
http://www.psynetresearch.org/informati ... ethod.html
http://www.mathsteacher.com.au/year8/ch ... q/freq.htm
http://math.tutorvista.com/statistics/f ... ution.html
http://www.mathsisfun.com/data/frequenc ... ution.html
http://www.mathsisfun.com/data/pie-charts.html
http://www.mathsisfun.com/data/bar-graphs.html
http://www.mathsisfun.com/data/histograms.html
practice test
http://www.shodor.org/interactivate/act ... /PieChart/
http://www.shodor.org/interactivate/act ... /BarGraph/
http://www.shodor.org/interactivate/act ... Histogram/
TOPIC:
Angles: Identification and properties of angles – vertically opposite angles, adjacent angles, alternate angles, corresponding angles.
CONTENTS
(i). Identification of angles.
(ii). Properties of angles.
Identification of angles:
When two lines meet at a point, they form an angle. An angle is defined as the amount that one line turns through to meet the other line.
The point B where two lines AB and CB meet is called the vertex. Lines AB and BC are called the arms of the angle. If the direction (turning) of a line is same as the direction of a clock then such rotation is called clockwise rotation. If the direction is in the opposite direction it is called as anti-clockwise or counter -clockwise rotation. In the drawing above, the angle at point B can be expressed as A(BC) ̂ or
B ̂ or ‹ABC or ‹CBA. (teacher to explain these notations ).
(ii). Properties of angles.
Definitions:
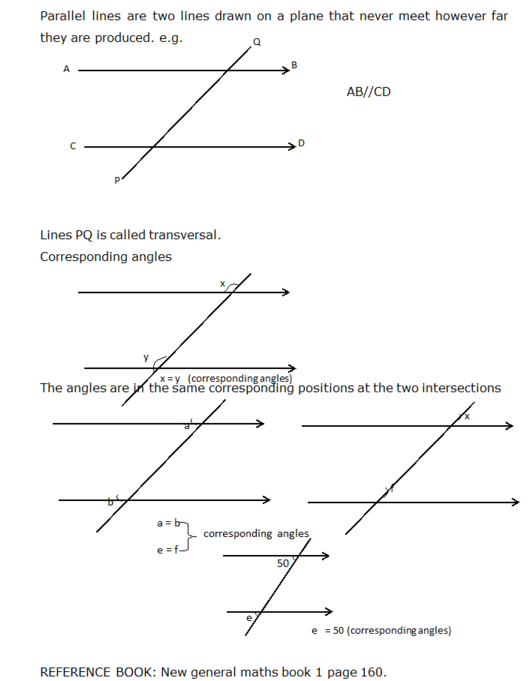
Any line drawn across set of parallel lines is referred to as a transversal.
Angles are said to be supplementary if their sum gives two right angles (〖180〗^0 )
Angles are said to be complementary if their sum gives one right angle (〖90〗^0 ).
When a transversal cuts across a set of parallel lines we have the following three principles or
laws of angles in display: Corresponding angles, Alternate angles, Co-Interior or Allied angles.
Notes: Corresponding angles are equal. Alternate angles are equal, but Co-interior or allied
angles are supplementary. These three laws require parallelism.
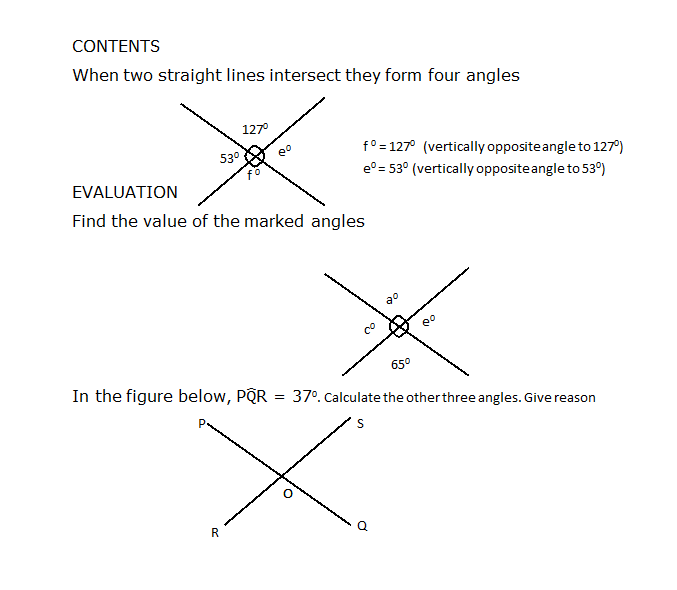
Vertically opposite angles
When two straight lines intersect, they form four angles; two angles opposite to each other are said to be vertically opposite.
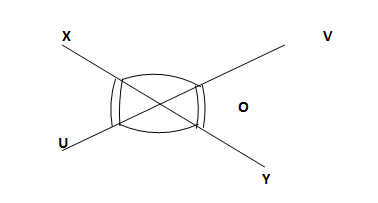
VOY.
Vertically opposite angles are equal. Hence, <XOV = <UOY; <XOU = <VOY.
CLASS ACTIVITY
Use your protractor to measure the following angles; <XOU, <XOV, <UOY and <VOY.
What do you notice?
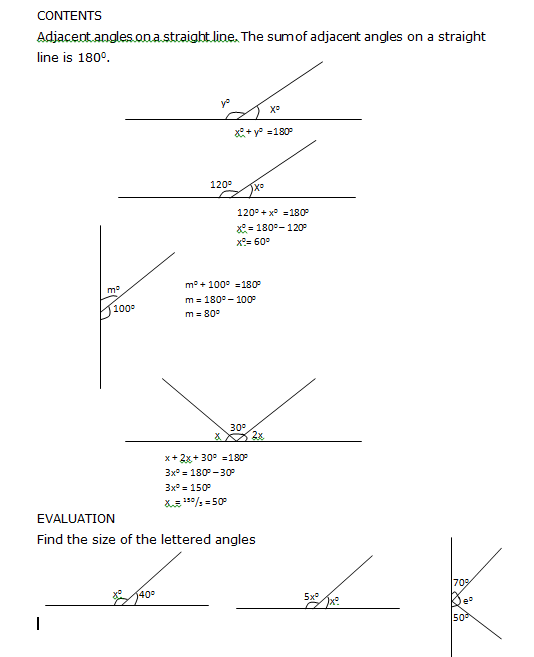
Adjacent angles on a straight line
In the diagram below, <XOY is a straight line, <XOZ and <YOZ lie next to each other, and they
are referred to as adjacent angles on a straight line. In other words, when two angles lie beside each other and have a common vertex, we say they are adjacent to each other.
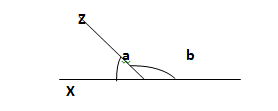
Since the sum of angles on a straight line is 1800 , <XOZ + <YOZ = 1800 . i.e. a + b = 1800
The sum of adjacent angles on a straight line is 1800 .
CLASS ACTIVITY
Use your protractor to measure angles labeled a and b.
Add angles a and b. What do you notice?
NOTE: Adjacent angles are said to be supplementary.
Alternate angles
Alternate angles are equal.

In the diagram drawn above a is alternate to b and r is alternate to s
CLASS ACTIVITY
Use your protractor to measure the angles labeled a, b, r and s.
What is your observation?
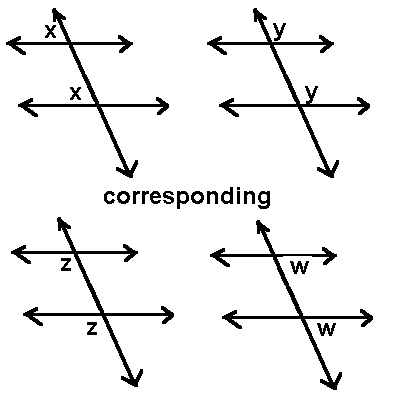
Corresponding angles
Corresponding angles are equal.
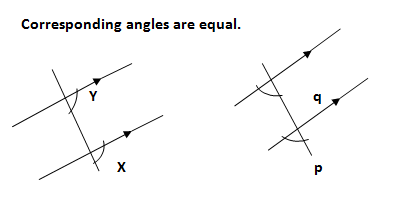
CLASS ACTIVITY
Use your protractor to measure the angles labeled x and y and then p and q in the in the diagram above. What do you notice?
NOTE: Angles x and y are called corresponding angles. Also angles p and q are called corresponding angles.
Therefore, when a transversal cut parallel lines corresponding angles formed are equal.
Reading Assignment:
New General Mathematics for Junior Secondary Schools 1. Pages 156 – 165.
Working Assignment
Assignment: New General Mathematics for Junior Secondary Schools 1. Ex. 20e and Ex. 20f.
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to construct a rhombus using rulers set squares and protractors.

CONTENTS
A rhombus is a parallelogram with all its sides the same length
Example: construct a rhombus with one angle of 450 and each side 4cm long
Rough sketch
Steps
1. Draw angle ABC = 450 so that arms BA and BC are 4cm each
2. Draw a line through C parallel to BA to make the rhombus ABCD
EVALUATION
a. Construct a rhombus with one angle of 650 and each side 4cm long.
b. Measure the angle between the diagonals
ASSIGNMENT
Construct a trapezium ABCD so that BC=6cm AB=3cm B=80 degrees and C= 70 degrees
further studies
http://mathandmultimedia.com/2011/01/09 ... 7-rhombus/
http://www.mathopenref.com/constangle30.html
watch video
http://www.youtube.com/watch?v=Gwkf_Fem2XI
LESSON 92
MAIN TOPIC: STATISTICS
SPECIFIC TOPIC: TYPES OF STATISTICAL PRESENTATION
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to interpret statistical data numerically and graphically
REFERENCE BOOK: New general maths for West Africa (JSS1) page 144
CONTENTS
Types of presentation
Data can be presented in the following ways:
a. Rank order list

b. Frequency table


c. Histogram

d. Bar chart

e. Pie chart

Example: An English teacher gave an essay to 15 students
She graded the essays from A (very good) through B, C, D, E, F (very poor) the grades of the students were: B, C,A,B,A,D,F,E,C,C,A,B,B,E,B
EVALUATION: (Oral)
New general maths for West Africa (JSS 1) page 145, Ex 18a. question 1,2,4,5
ASSIGNMENT: (Written)
New general maths for West Africa (JSS 1) page 147; exercise 18b question 11 and 12
further studies
http://www.scribd.com/doc/47650615/Stat ... tion-Tools
http://www.psynetresearch.org/informati ... ethod.html
http://www.mathsteacher.com.au/year8/ch ... q/freq.htm
http://math.tutorvista.com/statistics/f ... ution.html
http://www.mathsisfun.com/data/frequenc ... ution.html
http://www.mathsisfun.com/data/pie-charts.html
http://www.mathsisfun.com/data/bar-graphs.html
http://www.mathsisfun.com/data/histograms.html
practice test
http://www.shodor.org/interactivate/act ... /PieChart/
http://www.shodor.org/interactivate/act ... /BarGraph/
http://www.shodor.org/interactivate/act ... Histogram/
TOPIC:
Angles: Identification and properties of angles – vertically opposite angles, adjacent angles, alternate angles, corresponding angles.
CONTENTS
(i). Identification of angles.
(ii). Properties of angles.
Identification of angles:
When two lines meet at a point, they form an angle. An angle is defined as the amount that one line turns through to meet the other line.


The point B where two lines AB and CB meet is called the vertex. Lines AB and BC are called the arms of the angle. If the direction (turning) of a line is same as the direction of a clock then such rotation is called clockwise rotation. If the direction is in the opposite direction it is called as anti-clockwise or counter -clockwise rotation. In the drawing above, the angle at point B can be expressed as A(BC) ̂ or
B ̂ or ‹ABC or ‹CBA. (teacher to explain these notations ).
(ii). Properties of angles.
Definitions:
Any line drawn across set of parallel lines is referred to as a transversal.
Angles are said to be supplementary if their sum gives two right angles (〖180〗^0 )
Angles are said to be complementary if their sum gives one right angle (〖90〗^0 ).
When a transversal cuts across a set of parallel lines we have the following three principles or
laws of angles in display: Corresponding angles, Alternate angles, Co-Interior or Allied angles.
Notes: Corresponding angles are equal. Alternate angles are equal, but Co-interior or allied
angles are supplementary. These three laws require parallelism.
Vertically opposite angles
When two straight lines intersect, they form four angles; two angles opposite to each other are said to be vertically opposite.

VOY.
Vertically opposite angles are equal. Hence, <XOV = <UOY; <XOU = <VOY.
CLASS ACTIVITY
Use your protractor to measure the following angles; <XOU, <XOV, <UOY and <VOY.
What do you notice?
Adjacent angles on a straight line
In the diagram below, <XOY is a straight line, <XOZ and <YOZ lie next to each other, and they
are referred to as adjacent angles on a straight line. In other words, when two angles lie beside each other and have a common vertex, we say they are adjacent to each other.

Since the sum of angles on a straight line is 1800 , <XOZ + <YOZ = 1800 . i.e. a + b = 1800
The sum of adjacent angles on a straight line is 1800 .
CLASS ACTIVITY
Use your protractor to measure angles labeled a and b.
Add angles a and b. What do you notice?
NOTE: Adjacent angles are said to be supplementary.
Alternate angles
Alternate angles are equal.

In the diagram drawn above a is alternate to b and r is alternate to s
CLASS ACTIVITY
Use your protractor to measure the angles labeled a, b, r and s.
What is your observation?
Corresponding angles
Corresponding angles are equal.

CLASS ACTIVITY
Use your protractor to measure the angles labeled x and y and then p and q in the in the diagram above. What do you notice?
NOTE: Angles x and y are called corresponding angles. Also angles p and q are called corresponding angles.
Therefore, when a transversal cut parallel lines corresponding angles formed are equal.
Reading Assignment:
New General Mathematics for Junior Secondary Schools 1. Pages 156 – 165.
Working Assignment
Assignment: New General Mathematics for Junior Secondary Schools 1. Ex. 20e and Ex. 20f.
WEEK 8
TOPIC : Identification of angles at a point and angles on a straight line. Sum of angles in a triangle.
Content:
• Identification of angles at a point
• Identification of angles on a straight line
• Sum of angles in a triangle.
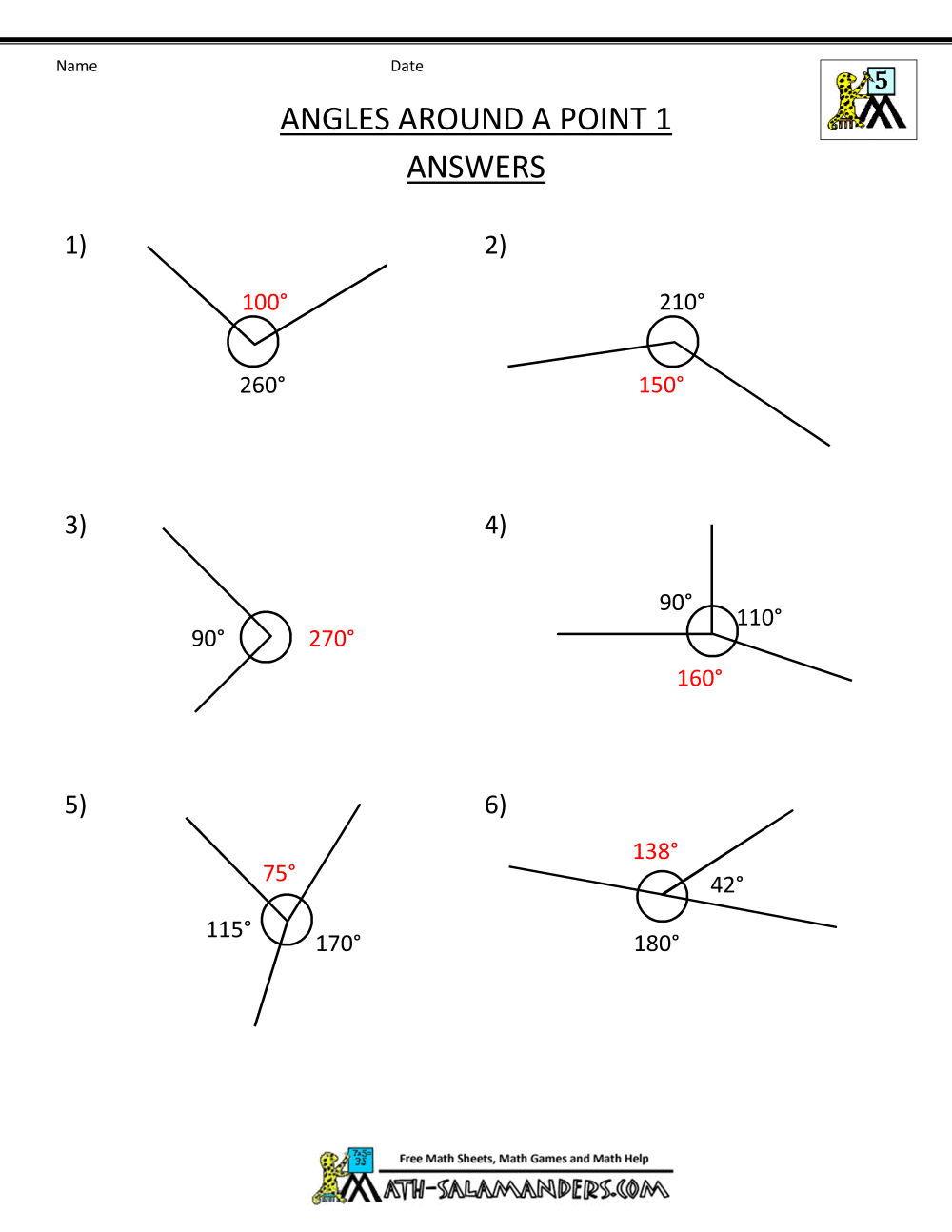
Identification of angles at a point
The sum of angles at a point is 3600 .
In the diagram below all the lines intersect at a point O.
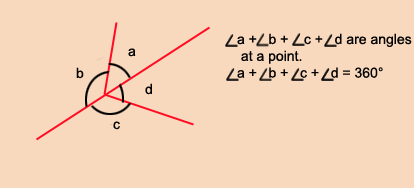
CLASS ACTIVITY
a. Use your protractor to measure angles labeled p, q, r and s.
b. Add angles p, q, r and s . what is your observation?
Note: From the activity above, your result should add up to 3600 .

EVALUATION:
(i). what do you understand by the following principles?
• Corresponding angles
• Alternate angles
• Co-Interior or Allied angles
• Vertically opposite angles
• Sum of angles on a straight line
• Angles at a point.
(ii) Make rough sketches to explain them.
Sum of angles in a triangle
The sum of angles in a triangle is 1800 .
To show this, draw line LM through the top vertex of the triangle, parallel to the base BC. Label each angle as shown in the diagram below.
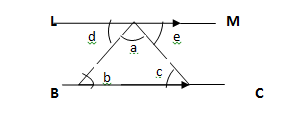
From the above diagram:
b = d (alternate angles)
c = e (alternate angles)
But d + a + e = 1800 (sum of angles on a straight line)
Since d + e = b + c
Hence: a + b + c = d + a + e = 1800
Thus, the sum of angles of a triangle = 1800 .
Worked Example
Find the size of angle x in this triangle
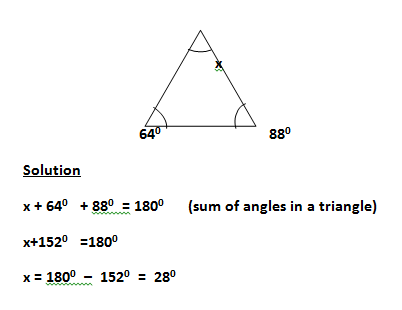
Reading Assignment: New General Mathematics for Junior Secondary Schools 1. Pages 156 – 162.
Week-end Assignment: New General Mathematics for Junior Secondary Schools 1. Ex. 20b, no 1-12, Ex. 20c no 1, Ex. 20e no 1 – 3 and Ex. 20h no 1 – 6.
Content:
• Identification of angles at a point
• Identification of angles on a straight line
• Sum of angles in a triangle.
Identification of angles at a point
The sum of angles at a point is 3600 .
In the diagram below all the lines intersect at a point O.

CLASS ACTIVITY
a. Use your protractor to measure angles labeled p, q, r and s.
b. Add angles p, q, r and s . what is your observation?
Note: From the activity above, your result should add up to 3600 .

EVALUATION:
(i). what do you understand by the following principles?
• Corresponding angles
• Alternate angles
• Co-Interior or Allied angles
• Vertically opposite angles
• Sum of angles on a straight line
• Angles at a point.
(ii) Make rough sketches to explain them.
Sum of angles in a triangle
The sum of angles in a triangle is 1800 .
To show this, draw line LM through the top vertex of the triangle, parallel to the base BC. Label each angle as shown in the diagram below.

From the above diagram:
b = d (alternate angles)
c = e (alternate angles)
But d + a + e = 1800 (sum of angles on a straight line)
Since d + e = b + c
Hence: a + b + c = d + a + e = 1800
Thus, the sum of angles of a triangle = 1800 .
Worked Example
Find the size of angle x in this triangle

Reading Assignment: New General Mathematics for Junior Secondary Schools 1. Pages 156 – 162.
Week-end Assignment: New General Mathematics for Junior Secondary Schools 1. Ex. 20b, no 1-12, Ex. 20c no 1, Ex. 20e no 1 – 3 and Ex. 20h no 1 – 6.
WEEK 9
TOPIC: Need for Statistics: Purpose of statistics. Need for collecting data for planning purposes. Need for collecting data for analysis purpose. Need for collecting data for prediction purposes.
CONTENT:
• Purpose of statistics.
• Need for collecting data for planning purposes.
• Need for collecting data for analysis purpose.
• Need for collecting data for prediction purposes.
Purpose of Statistics
Statistics is the branch of mathematics, which deals with the study of data. It involves:
a. Gathering (i.e. collecting) data
b. Sorting and tabulating data
c. Presenting data visually by means of diagrams
d. Interpreting results.
Statistics is known to provide useful information in our everyday life:
For record keeping
To forecast or predict future events
For decision making
For planning purposes
To gather useful information this can be passed from one source to another.
CLASS ACTIVITY
1. Find out the number of students in your school. Make a table to show the number of students in each level
2. How many males and female students do you have in your school?
3. How many male and female teachers are in your school?
Need for collecting data for planning purposes
The daily export report of barrels of petrol enables the government of Nigeria to plan the budgets. This is called economic planning.
Example 1:
A shop keeper makes record of his sales for the day. The records are as shown in the table below. This is an example of statistics used for planning purpose/decision making.

Which size sells more than the other?
Which size gives more profit for the day?
If you were the shop keeper, which size would you plan to buy more on the following day? Give reasons.
Need for collecting data for analysis purpose
Collection of data from time to time helps to analyze situations. For example, statistics shows that malaria is responsible for about half the deaths of African children under the age of five. The minister of health in Nigeria revealed that the number of tuberculosis in Nigeria increased from 31 264 in 2002 to 90 307 in 2008. The number of people who died of Aids in South Africa in 2007 is about 350 000. This means Aids claimed nearly 1000 lives every day.
Example 2:
The table below shows a survey of the favourite subjects of students in basic 2.

Need for collecting data for prediction purposes
The statistical charts and tables we do see on television and in the newspapers (or magazines), provide useful information which can be used to make forecast and predictions for the future. For example, the number of students enrolment in secondary and post secondary schools this year can help the government plans the number of new jobs to be created in five years’ time.
Example 3:
A food seller collects the following sales data for the week.
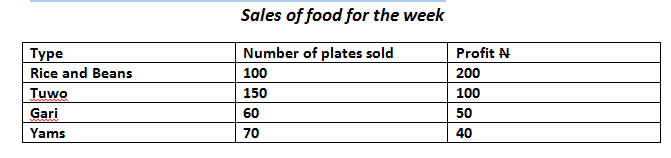
Will you support her decision to stop selling tuwo and yam? On what prediction do you think she based her decision?
EVALUATION QUESTION
1. If your village played with another village 10 times in the past, with 9 wins and 1 loss, what is your prediction for the next match?
2. Give some reasons why you think a school principal should know the number of students in the his school?
Reading Assignment: New General Mathematics for Junior Secondary Schools 1. Pages 139 – 144.
Working Assignment: New General Mathematics for Junior Secondary Schools 1. Ex. 18a no 1,2 and 4.
TOPIC: Data collection: collection of data in the class. Median – Determining the median of a given set of data.
CONTENT:
Collection of data in the class
Median – Determining the median of a given set of data.
Collection of data in the class
Ability to count and write or record data clearly is the basic requirement to for effective data collection.
Example 1:
In a class of 30 students seated in six rows of five students each, the class monitor records the following dates of births, row by row.
Wed. Thur. Sun. Tue Fri.
Mon. Wed. Tues. Fri. Sun.
Sun. Wed. Mon Tues. Sat.
Fri. Sat. Sun. Thur. Wed.
Mon. Sat. Sun. Fri. Mon
Dates of birth of 30 Students
How many students were born on Tuesdays?
In what date were most students born?
In what date were the least number of students born?
Solution
The above data can be collected in a very simple and better way as shown below.
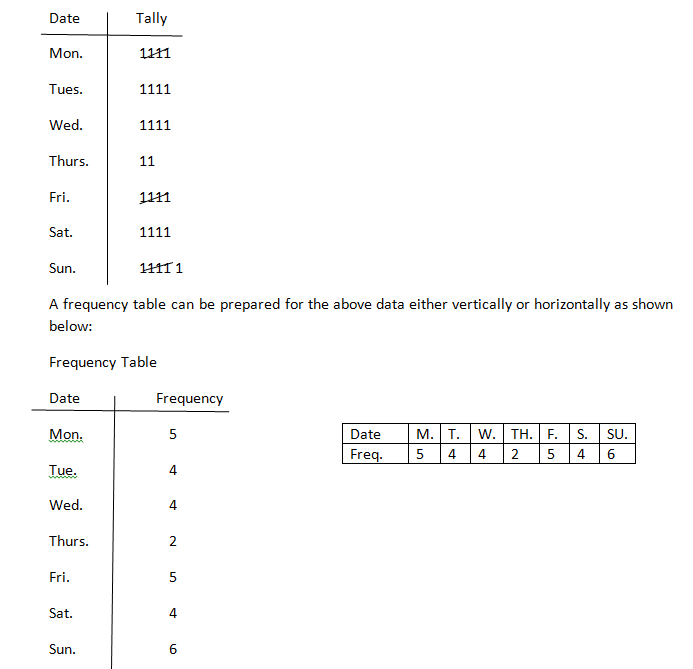
Examples 2:
Two students were asked to collect data about the type of vehicles, as they passed by. The data collected were presented in two different ways.
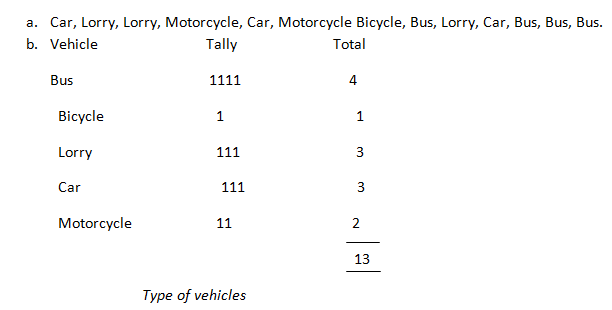
The first student presented his data by listing the vehicles as they pass by. This method is not very reliable. The method adopted by the second student is the best because he cannot miss any vehicle in his recording.
Determining the Median of a given set of data
The median of a set of values or data is the middle value when the data is arranged in order of magnitude or size.
Worked example1:
Find the median of these numbers:
13, 15, 14, 12, 13, 15, 16, 10, 12, 14

CLASS ACTIVITY
Obtain the weight and the height of students in your class. Then calculate the median weight.
EVALUATION QUESTIONS.
Find the median of these numbers:
5.5, 8.6, 4.8, 10.5, 6.8, 7.5, 8.2
50%, 55%, 60%, 70%, 65%
-30C, -20C, 00C, 40C, -40C, -10C, 20C, -20C, 10C, -10C. (View Correctly Below)
2, 8, 9, 12, 7, 5, 6, 4, 5, 10, 11, 3, 6.

Reading Assignment:
New General Mathematics for Junior Secondary Schools 1. Pages 171 - 173.
Working Assignment:
New General Mathematics for Junior Secondary Schools 1. Page 174 – 175. Ex. 22d no 3 – 7.
CONTENT:
• Purpose of statistics.
• Need for collecting data for planning purposes.
• Need for collecting data for analysis purpose.
• Need for collecting data for prediction purposes.
Purpose of Statistics
Statistics is the branch of mathematics, which deals with the study of data. It involves:
a. Gathering (i.e. collecting) data
b. Sorting and tabulating data
c. Presenting data visually by means of diagrams
d. Interpreting results.
Statistics is known to provide useful information in our everyday life:
For record keeping
To forecast or predict future events
For decision making
For planning purposes
To gather useful information this can be passed from one source to another.
CLASS ACTIVITY
1. Find out the number of students in your school. Make a table to show the number of students in each level
2. How many males and female students do you have in your school?
3. How many male and female teachers are in your school?
Need for collecting data for planning purposes
The daily export report of barrels of petrol enables the government of Nigeria to plan the budgets. This is called economic planning.
Example 1:
A shop keeper makes record of his sales for the day. The records are as shown in the table below. This is an example of statistics used for planning purpose/decision making.

Which size sells more than the other?
Which size gives more profit for the day?
If you were the shop keeper, which size would you plan to buy more on the following day? Give reasons.
Need for collecting data for analysis purpose
Collection of data from time to time helps to analyze situations. For example, statistics shows that malaria is responsible for about half the deaths of African children under the age of five. The minister of health in Nigeria revealed that the number of tuberculosis in Nigeria increased from 31 264 in 2002 to 90 307 in 2008. The number of people who died of Aids in South Africa in 2007 is about 350 000. This means Aids claimed nearly 1000 lives every day.
Example 2:
The table below shows a survey of the favourite subjects of students in basic 2.

Need for collecting data for prediction purposes
The statistical charts and tables we do see on television and in the newspapers (or magazines), provide useful information which can be used to make forecast and predictions for the future. For example, the number of students enrolment in secondary and post secondary schools this year can help the government plans the number of new jobs to be created in five years’ time.
Example 3:
A food seller collects the following sales data for the week.

Will you support her decision to stop selling tuwo and yam? On what prediction do you think she based her decision?
EVALUATION QUESTION
1. If your village played with another village 10 times in the past, with 9 wins and 1 loss, what is your prediction for the next match?
2. Give some reasons why you think a school principal should know the number of students in the his school?
Reading Assignment: New General Mathematics for Junior Secondary Schools 1. Pages 139 – 144.
Working Assignment: New General Mathematics for Junior Secondary Schools 1. Ex. 18a no 1,2 and 4.
TOPIC: Data collection: collection of data in the class. Median – Determining the median of a given set of data.
CONTENT:
Collection of data in the class
Median – Determining the median of a given set of data.
Collection of data in the class
Ability to count and write or record data clearly is the basic requirement to for effective data collection.
Example 1:
In a class of 30 students seated in six rows of five students each, the class monitor records the following dates of births, row by row.
Wed. Thur. Sun. Tue Fri.
Mon. Wed. Tues. Fri. Sun.
Sun. Wed. Mon Tues. Sat.
Fri. Sat. Sun. Thur. Wed.
Mon. Sat. Sun. Fri. Mon
Dates of birth of 30 Students
How many students were born on Tuesdays?
In what date were most students born?
In what date were the least number of students born?
Solution
The above data can be collected in a very simple and better way as shown below.

Examples 2:
Two students were asked to collect data about the type of vehicles, as they passed by. The data collected were presented in two different ways.

The first student presented his data by listing the vehicles as they pass by. This method is not very reliable. The method adopted by the second student is the best because he cannot miss any vehicle in his recording.
Determining the Median of a given set of data
The median of a set of values or data is the middle value when the data is arranged in order of magnitude or size.
Worked example1:
Find the median of these numbers:
13, 15, 14, 12, 13, 15, 16, 10, 12, 14

CLASS ACTIVITY
Obtain the weight and the height of students in your class. Then calculate the median weight.
EVALUATION QUESTIONS.
Find the median of these numbers:
5.5, 8.6, 4.8, 10.5, 6.8, 7.5, 8.2
50%, 55%, 60%, 70%, 65%
-30C, -20C, 00C, 40C, -40C, -10C, 20C, -20C, 10C, -10C. (View Correctly Below)
2, 8, 9, 12, 7, 5, 6, 4, 5, 10, 11, 3, 6.

Reading Assignment:
New General Mathematics for Junior Secondary Schools 1. Pages 171 - 173.
Working Assignment:
New General Mathematics for Junior Secondary Schools 1. Page 174 – 175. Ex. 22d no 3 – 7.
