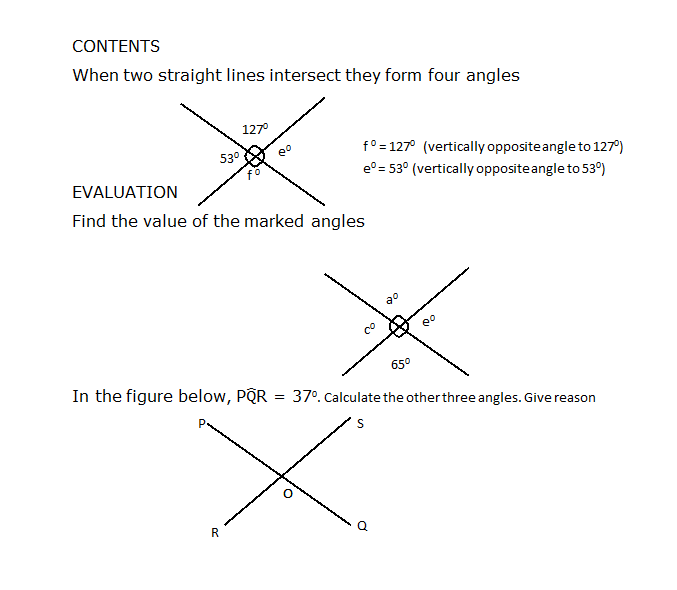
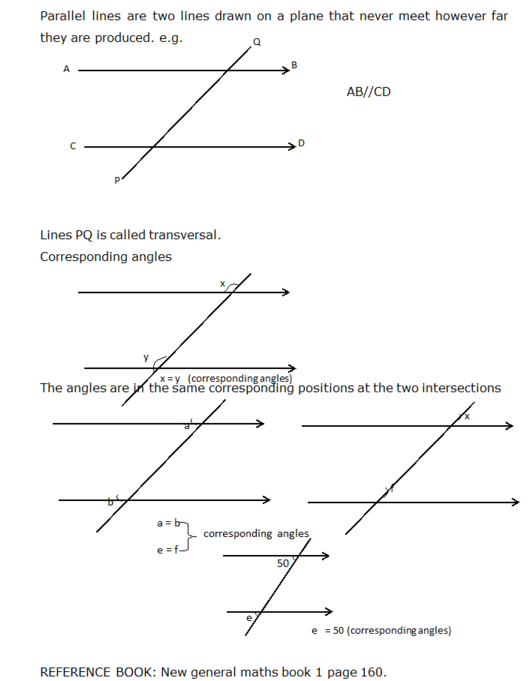
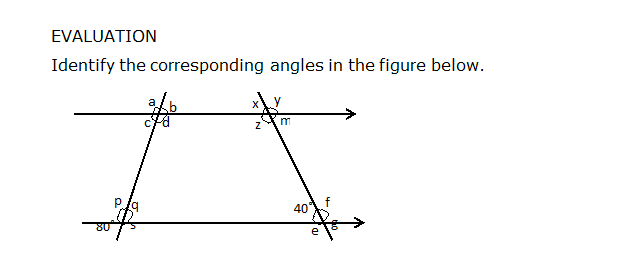
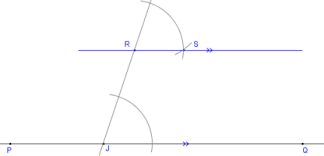
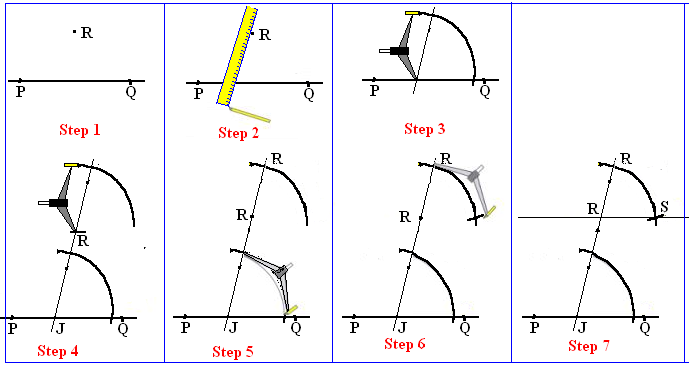
Topic : Geometry- plane shapes
Contents:
Perimeter of a regular polygon
Perimeter of a square
Perimeter of a rectangle
Perimeter of a triangle
Perimeter of a trapezium
Perimeter of a parallelogram
Perimeter of a circle
MEASURING PERIMETERS
Perimeter is the outside boundary or edge of a plane shape. For example, the boundary fence of your school compound is its perimeter. We also use the word perimeter to mean the length of the boundary. For example , if you take 200 paces to walk your school boundary, you could say its perimeter is 200 paces.
PERIMETER OF A REGULAR POLYGON
The simplest way to find a perimeter of any regular shape is to measure it directly with a ruler. Or tape measure.
Examples;
Find, in cm the perimeter of the regular hexagon ABCDEF in Fig. 1.0.
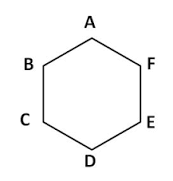
Length of side AB = 1.6 cm.
There are 6 equal sides, so
Perimeter = 6 × 1.6cm
=9.6 cm
If a shape has a curved side, use a piece of thread to get the shape of the curve. Make the thread to get the shape of the curve. Make the thread straight and measure its length against a ruler.
2. Measure the Perimeter of the shape in the fig below.
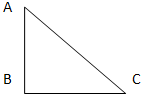
Straight edges: AB = 14 mm =1.4 cm
BC =14 mm =1.4 cm
Curved edge: CA =22mm approximately
=2.2cm
Perimeter (total = 50 mm approximately
= 5.0 cm
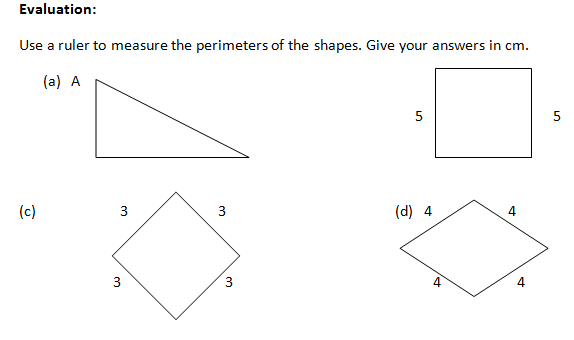
Evaluation:
Draw and Use a ruler to measure the perimeters of the shape illustrated above. Give your answer in cm.
(a)
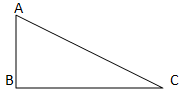
Straight edges : AB = 14 mm = 1.4 cm
BC = 14mm = 1.4 cm
Curved edge : CA = 22 mm approximately
= 2.2 cm
Perimeter (total ) = 50 mm approximately
= 5.0 cm
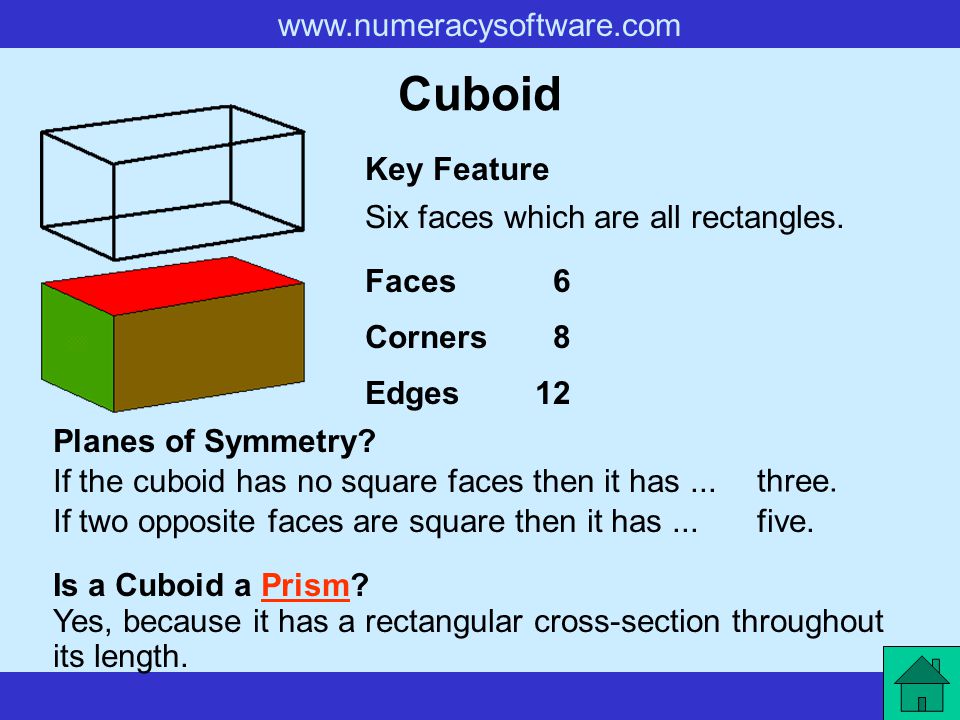
PERIMETER OF A SQUARE
A square is a regular four- sided shape. If the length of one side of a square is l, then,
Perimeter of square = l × 4
= 4l
As perimeter of square =4l,
Length of side of square = perimeter of square
4
Example ;
(1) Calculate the perimeter of a square of side 12.3cm.
Solution
Perimeter = 12.3cm × 4
Perimeter = 49.2 cm
(2) A square assembly area has a perimeter of 56m. Find the length of the assembly area.
Solution
Length = 56
4
= 14m.
Note: The formulae for perimeters of rectangles and squares can be useful. However, if you find it difficult to remember formulae, always sketch the given shape and work from that.

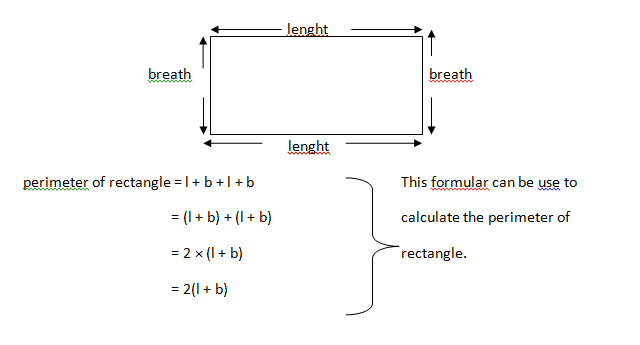
PERIMETER OF RECTANGLES
The longer side of a rectangle is called length , and the shorter side is calledbreadth . We use the letter l and b to stand for the length and the breath.
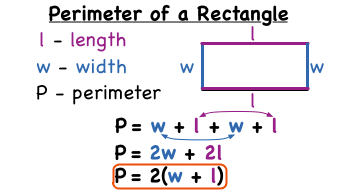
perimeter of rectangle = l + b + l + b This formular can be use to
= (l + b) + (l + b) calculate the perimeter of
= 2 × (l + b) rectangle.
= 2(l + b)
Example
Calculate the perimeter of a football field which measures 80m by 50m.
Solution
Perimeter of field = 2(l+ b)
= 2 × (80 + 50) m
= 2 × 130m
= 260m.
(3) A rectangular piece of land measures 57 m by 42m. What is the perimeter of the perimeter of the land ?
Perimeter of land = 2(l+ b)
= 2(57+ 45)m
= 2× 99m
= 198m.
AREA OF A TRIANGLES
Any diagonal of a rectangle divided it into two equal right- angled triangles.
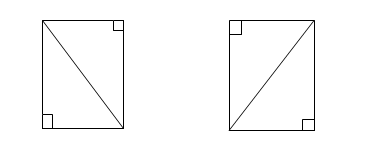
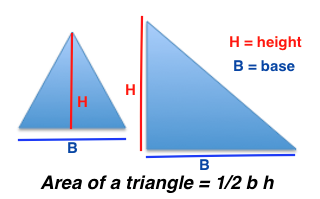
Thus :
Area of a right – angled triangle
= ½ × product of sides containing the right angle.
Area of triangle = ½ × base × height.
Example:
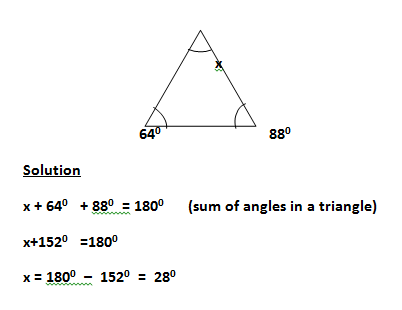
Calculate the area of the triangle shown below;
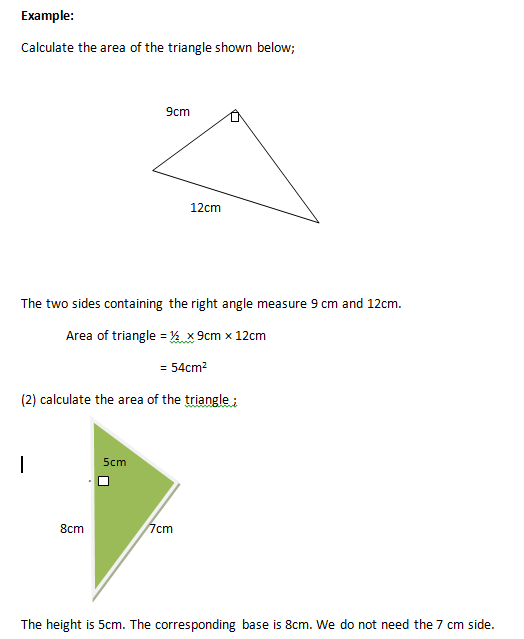
The two sides containing the right angle measure 9 cm and 12cm.
Area of triangle = ½ × 9cm × 12cm
= 54cm2
(2) calculate the area of the triangle with height 5cm, base 8cm and hypotenuse 7cm.
The height is 5cm. The corresponding base is 8cm. We do not need the 7 cm side.
Solution:
Area of triangle = ½ ×base × height
= ½ × 8cm × 5cm
= 20cm2
Evaluation:
New general mathematics for junior secondary schools 1 UBE Edition.
Exercise 14d 1(a) –(d) page 120.
AREA OF A TRAPEZIUMS:

ABCD is a trapezium in which AB is parallel to DC. The diagonal AD divides the trapezium into two triangles. The height, h, is the same for both triangles.
area of trapezium ABCD
= area of ABD + area of BDC
½ AB × h + ½ DC × h
= ½ (AB + DC)h
Example:
Calculate the area of the trapezium ABCD in figure below;
The diagonal AC divides the trapezium into two triangles. The height of each triangle is 8 cm.
Area of ACB = ½ × 13cm × 8cm =52cm2
Area of ACD = ½ × 6cm × 8cm = 24cm2
Area of trapezium = 52cm2 + 24cm2 =76cm2
Evaluation:
New general mathematics for junior secondary school 1 UBE Edition,
Exercise : 14d no’s: 2(a) – (d).
Area of parallelograms
A parallelogram can have two bases and two corresponding heights as show below;
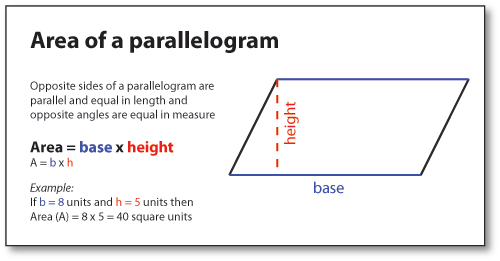
Area (A) = base (1) × height (1)
Also area (A) =base(2) × height (2)
Therefore base (1) × height (2) × height (2)
Example:
Calculate the area of the paralellograms below. All dimensions are in centimeters.
base = 5
height = 7
(a) Area of parallelogram = base × height
= 7cm × 5 cm
= 35cm
base = 5
height = 3
(b) Area of parallelogram = base × height
= 5cm × 3cm
= 15cm.
Evaluation:
1. Calculate the area of a parallelogram if its base is 9.2cm and its height is 6cm
2. the area of a parallelogram is 99cm2 its base is 11cm. calculate the corresponding height of the parallogram
3. calculate the base of a parallelogram whose area and height is 27cm and 9cm respectively.
Area of a circles
Area of a circle = ∏r2
∏ = 22/7
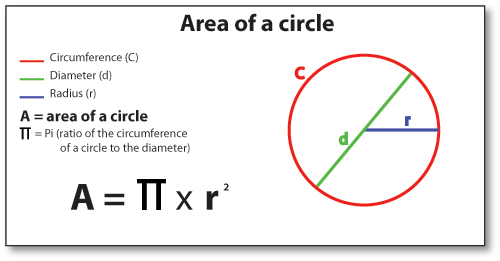
Diameter= 2r. where r = radius
Example:
(1) Find the area of a circle whose radius is 3½m. Taken∏to be 22/7
Solution:
area of a circle = ∏r2
= 22/7 × (3½)2= 22/7 × 7/2 × 7/2m2
= 11 × 7
2
= 381/2 m2

Evaluation:
New general mathematics for junior secondary schools 1 UBE Edition . Exercise 14e 1(a)- (f) page 122. take ∏= 22/7
Reading assignment:
New general mathematics for junior secondary schools 1 UBE Edition. Page 116- 123.
assignment:
New general mathematics for junior secondary schools 1 UBE Edition. Page116 -123. Exercise 14e 3(a) –(f), Exercise 14d 1 (a) – (e).